On Gaussian Markov models for conditional independence
Paper and Code
Dec 14, 2017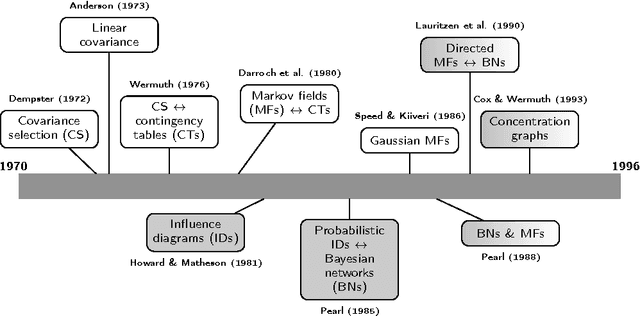

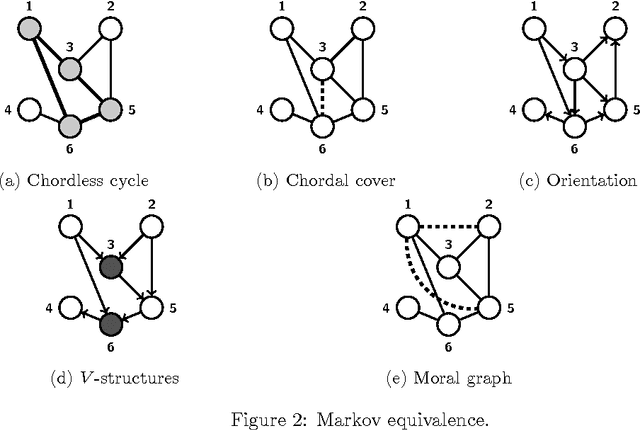

Markov models lie at the interface between statistical independence in a probability distribution and graph separation properties. We review model selection and estimation in directed and undirected Markov models with Gaussian parametrization, emphasizing the main similarities and differences. These two models are similar but not equivalent, although they share a common intersection. We present the existing results from a historical perspective, taking into account the amount of literature existing from both the artificial intelligence and statistics research communities, where these models were originated. We also discuss how the Gaussian assumption can be relaxed. We finally point out the main areas of application where these Markov models are nowadays used.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge