Sparse Cholesky covariance parametrization for recovering latent structure in ordered data
Paper and Code
Jun 02, 2020

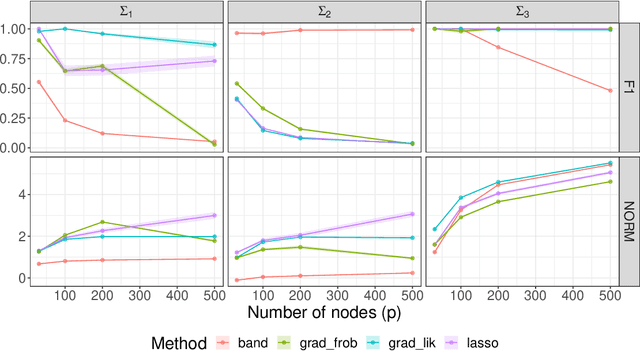
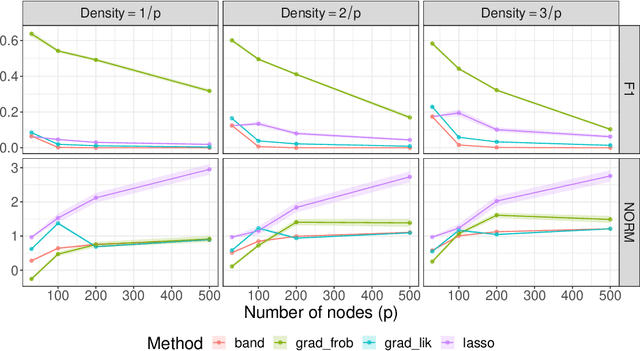
The sparse Cholesky parametrization of the inverse covariance matrix can be interpreted as a Gaussian Bayesian network; however its counterpart, the covariance Cholesky factor, has received, with few notable exceptions, little attention so far, despite having a natural interpretation as a hidden variable model for ordered signal data. To fill this gap, in this paper we focus on arbitrary zero patterns in the Cholesky factor of a covariance matrix. We discuss how these models can also be extended, in analogy with Gaussian Bayesian networks, to data where no apparent order is available. For the ordered scenario, we propose a novel estimation method that is based on matrix loss penalization, as opposed to the existing regression-based approaches. The performance of this sparse model for the Cholesky factor, together with our novel estimator, is assessed in a simulation setting, as well as over spatial and temporal real data where a natural ordering arises among the variables. We give guidelines, based on the empirical results, about which of the methods analysed is more appropriate for each setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge