Sparse Cholesky covariance parametrization for recovering latent structure in ordered data

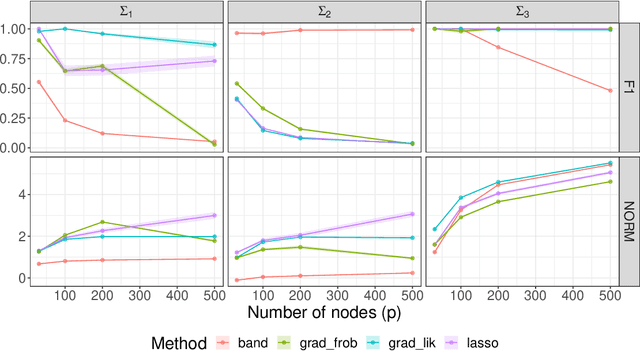
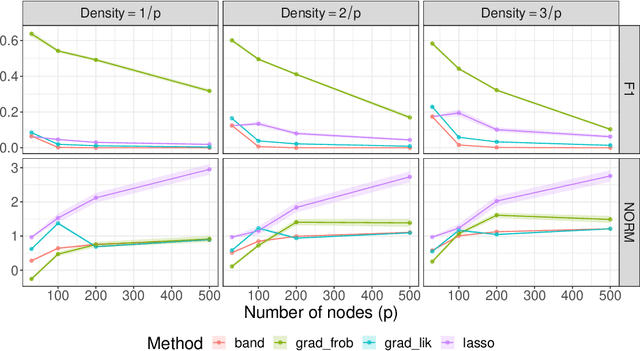
The sparse Cholesky parametrization of the inverse covariance matrix can be interpreted as a Gaussian Bayesian network; however its counterpart, the covariance Cholesky factor, has received, with few notable exceptions, little attention so far, despite having a natural interpretation as a hidden variable model for ordered signal data. To fill this gap, in this paper we focus on arbitrary zero patterns in the Cholesky factor of a covariance matrix. We discuss how these models can also be extended, in analogy with Gaussian Bayesian networks, to data where no apparent order is available. For the ordered scenario, we propose a novel estimation method that is based on matrix loss penalization, as opposed to the existing regression-based approaches. The performance of this sparse model for the Cholesky factor, together with our novel estimator, is assessed in a simulation setting, as well as over spatial and temporal real data where a natural ordering arises among the variables. We give guidelines, based on the empirical results, about which of the methods analysed is more appropriate for each setting.

Towards Gaussian Bayesian Network Fusion

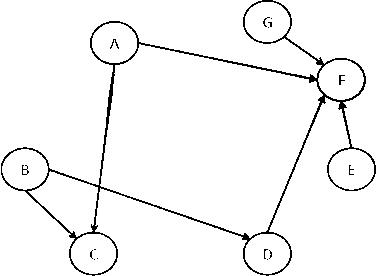
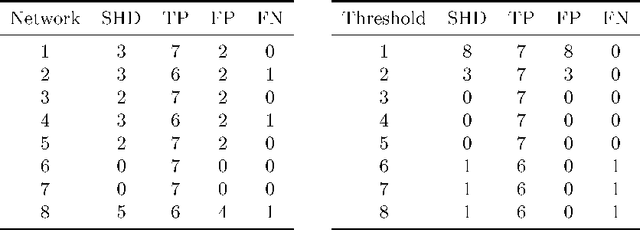
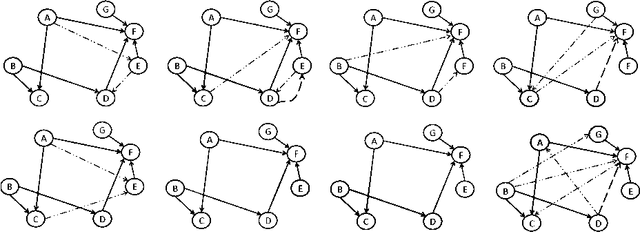
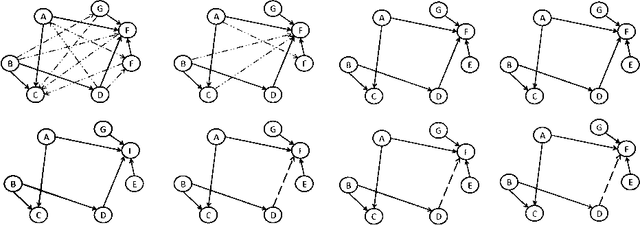
Data sets are growing in complexity thanks to the increasing facilities we have nowadays to both generate and store data. This poses many challenges to machine learning that are leading to the proposal of new methods and paradigms, in order to be able to deal with what is nowadays referred to as Big Data. In this paper we propose a method for the aggregation of different Bayesian network structures that have been learned from separate data sets, as a first step towards mining data sets that need to be partitioned in an horizontal way, i.e. with respect to the instances, in order to be processed. Considerations that should be taken into account when dealing with this situation are discussed. Scalable learning of Bayesian networks is slowly emerging, and our method constitutes one of the first insights into Gaussian Bayesian network aggregation from different sources. Tested on synthetic data it obtains good results that surpass those from individual learning. Future research will be focused on expanding the method and testing more diverse data sets.

Bayesian optimization of the PC algorithm for learning Gaussian Bayesian networks

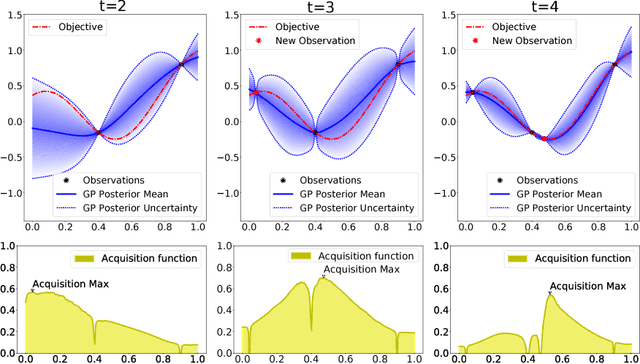
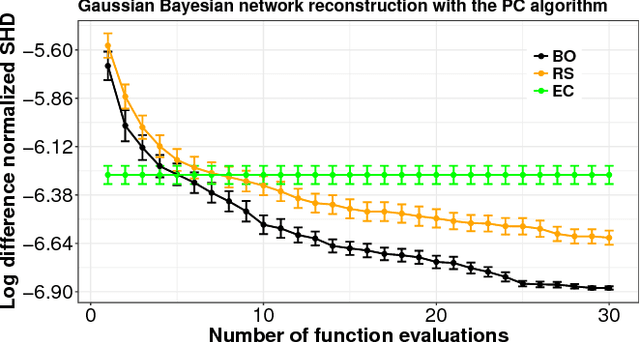
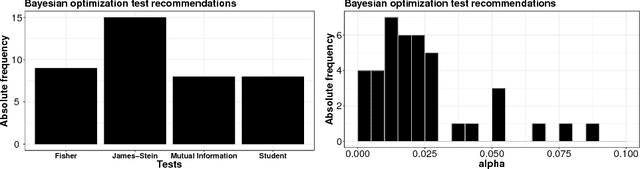
The PC algorithm is a popular method for learning the structure of Gaussian Bayesian networks. It carries out statistical tests to determine absent edges in the network. It is hence governed by two parameters: (i) The type of test, and (ii) its significance level. These parameters are usually set to values recommended by an expert. Nevertheless, such an approach can suffer from human bias, leading to suboptimal reconstruction results. In this paper we consider a more principled approach for choosing these parameters in an automatic way. For this we optimize a reconstruction score evaluated on a set of different Gaussian Bayesian networks. This objective is expensive to evaluate and lacks a closed-form expression, which means that Bayesian optimization (BO) is a natural choice. BO methods use a model to guide the search and are hence able to exploit smoothness properties of the objective surface. We show that the parameters found by a BO method outperform those found by a random search strategy and the expert recommendation. Importantly, we have found that an often overlooked statistical test provides the best over-all reconstruction results.