Semiparametric Bayesian Networks
Paper and Code
Sep 07, 2021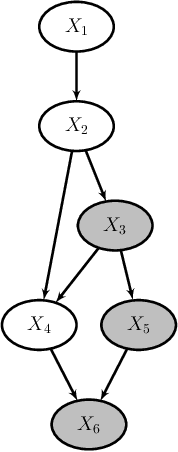
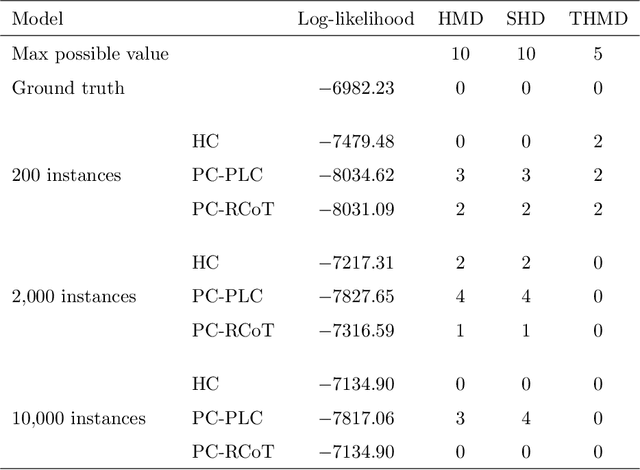
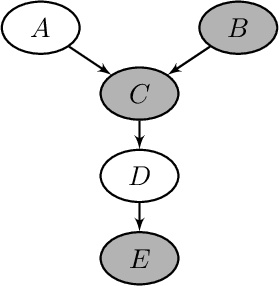
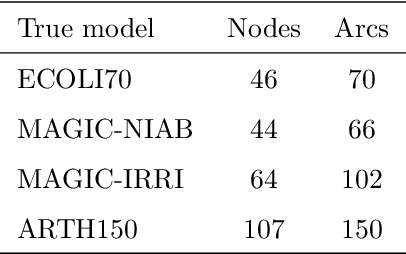
We introduce semiparametric Bayesian networks that combine parametric and nonparametric conditional probability distributions. Their aim is to incorporate the advantages of both components: the bounded complexity of parametric models and the flexibility of nonparametric ones. We demonstrate that semiparametric Bayesian networks generalize two well-known types of Bayesian networks: Gaussian Bayesian networks and kernel density estimation Bayesian networks. For this purpose, we consider two different conditional probability distributions required in a semiparametric Bayesian network. In addition, we present modifications of two well-known algorithms (greedy hill-climbing and PC) to learn the structure of a semiparametric Bayesian network from data. To realize this, we employ a score function based on cross-validation. In addition, using a validation dataset, we apply an early-stopping criterion to avoid overfitting. To evaluate the applicability of the proposed algorithm, we conduct an exhaustive experiment on synthetic data sampled by mixing linear and nonlinear functions, multivariate normal data sampled from Gaussian Bayesian networks, real data from the UCI repository, and bearings degradation data. As a result of this experiment, we conclude that the proposed algorithm accurately learns the combination of parametric and nonparametric components, while achieving a performance comparable with those provided by state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge