Task complexity shapes internal representations and robustness in neural networks

Neural networks excel across a wide range of tasks, yet remain black boxes. In particular, how their internal representations are shaped by the complexity of the input data and the problems they solve remains obscure. In this work, we introduce a suite of five data-agnostic probes-pruning, binarization, noise injection, sign flipping, and bipartite network randomization-to quantify how task difficulty influences the topology and robustness of representations in multilayer perceptrons (MLPs). MLPs are represented as signed, weighted bipartite graphs from a network science perspective. We contrast easy and hard classification tasks on the MNIST and Fashion-MNIST datasets. We show that binarizing weights in hard-task models collapses accuracy to chance, whereas easy-task models remain robust. We also find that pruning low-magnitude edges in binarized hard-task models reveals a sharp phase-transition in performance. Moreover, moderate noise injection can enhance accuracy, resembling a stochastic-resonance effect linked to optimal sign flips of small-magnitude weights. Finally, preserving only the sign structure-instead of precise weight magnitudes-through bipartite network randomizations suffices to maintain high accuracy. These phenomena define a model- and modality-agnostic measure of task complexity: the performance gap between full-precision and binarized or shuffled neural network performance. Our findings highlight the crucial role of signed bipartite topology in learned representations and suggest practical strategies for model compression and interpretability that align with task complexity.

Parallel Algorithms for Median Consensus Clustering in Complex Networks

We develop an algorithm that finds the consensus of many different clustering solutions of a graph. We formulate the problem as a median set partitioning problem and propose a greedy optimization technique. Unlike other approaches that find median set partitions, our algorithm takes graph structure into account and finds a comparable quality solution much faster than the other approaches. For graphs with known communities, our consensus partition captures the actual community structure more accurately than alternative approaches. To make it applicable to large graphs, we remove sequential dependencies from our algorithm and design a parallel algorithm. Our parallel algorithm achieves 35x speedup when utilizing 64 processing cores for large real-world graphs from single-cell experiments.

Community detection in networks using graph embeddings

Graph embedding methods are becoming increasingly popular in the machine learning community, where they are widely used for tasks such as node classification and link prediction. Embedding graphs in geometric spaces should aid the identification of network communities as well, because nodes in the same community should be projected close to each other in the geometric space, where they can be detected via standard data clustering algorithms. In this paper, we test the ability of several graph embedding techniques to detect communities on benchmark graphs. We compare their performance against that of traditional community detection algorithms. We find that the performance is comparable, if the parameters of the embedding techniques are suitably chosen. However, the optimal parameter set varies with the specific features of the benchmark graphs, like their size, whereas popular community detection algorithms do not require any parameter. So it is not possible to indicate beforehand good parameter sets for the analysis of real networks. This finding, along with the high computational cost of embedding a network and grouping the points, suggests that, for community detection, current embedding techniques do not represent an improvement over network clustering algorithms.

Classical Information Theory of Networks

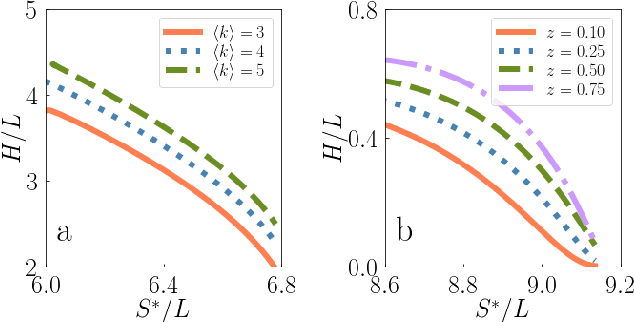
Heterogeneity is among the most important features characterizing real-world networks. Empirical evidence in support of this fact is unquestionable. Existing theoretical frameworks justify heterogeneity in networks as a convenient way to enhance desirable systemic features, such as robustness, synchronizability and navigability. However, a unifying information theory able to explain the natural emergence of heterogeneity in complex networks does not yet exist. Here, we fill this gap of knowledge by developing a classical information theoretical framework for networks. We show that among all degree distributions that can be used to generate random networks, the one emerging from the principle of maximum entropy is a power law. We also study spatially embedded networks finding that the interactions between nodes naturally lead to nonuniform distributions of points in the space. The pertinent features of real-world air transportation networks are well described by the proposed framework.