Aiiad Albeshri
Robustness modularity in complex networks
Oct 05, 2021

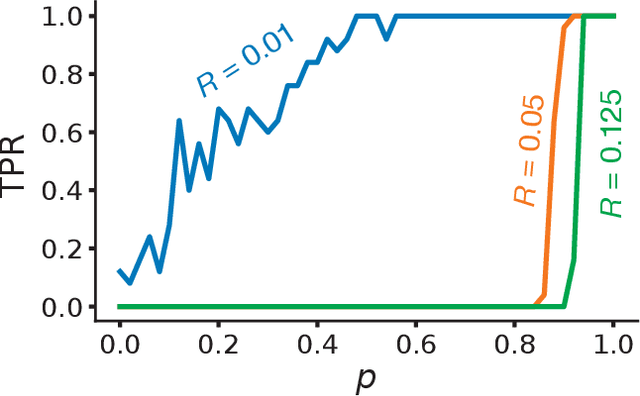
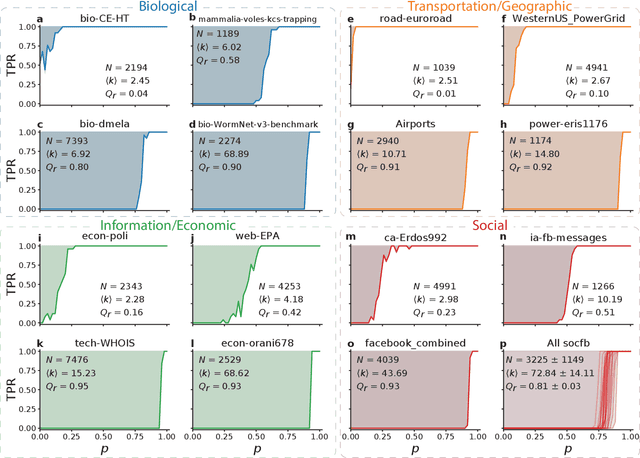
Abstract:A basic question in network community detection is how modular a given network is. This is usually addressed by evaluating the quality of partitions detected in the network. The Girvan-Newman (GN) modularity function is the standard way to make this assessment, but it has a number of drawbacks. Most importantly, it is not clearly interpretable, given that the measure can take relatively large values on partitions of random networks without communities. Here we propose a new measure based on the concept of robustness: modularity is the probability to find trivial partitions when the structure of the network is randomly perturbed. This concept can be implemented for any clustering algorithm capable of telling when a group structure is absent. Tests on artificial and real graphs reveal that robustness modularity can be used to assess and compare the strength of the community structure of different networks. We also introduce two other quality functions: modularity difference, a suitably normalized version of the GN modularity; information modularity, a measure of distance based on information compression. Both measures are strongly correlated with robustness modularity, and are promising options as well.
Community detection in networks using graph embeddings
Sep 11, 2020



Abstract:Graph embedding methods are becoming increasingly popular in the machine learning community, where they are widely used for tasks such as node classification and link prediction. Embedding graphs in geometric spaces should aid the identification of network communities as well, because nodes in the same community should be projected close to each other in the geometric space, where they can be detected via standard data clustering algorithms. In this paper, we test the ability of several graph embedding techniques to detect communities on benchmark graphs. We compare their performance against that of traditional community detection algorithms. We find that the performance is comparable, if the parameters of the embedding techniques are suitably chosen. However, the optimal parameter set varies with the specific features of the benchmark graphs, like their size, whereas popular community detection algorithms do not require any parameter. So it is not possible to indicate beforehand good parameter sets for the analysis of real networks. This finding, along with the high computational cost of embedding a network and grouping the points, suggests that, for community detection, current embedding techniques do not represent an improvement over network clustering algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge