The spectral dimension of simplicial complexes: a renormalization group theory
Paper and Code
Dec 09, 2019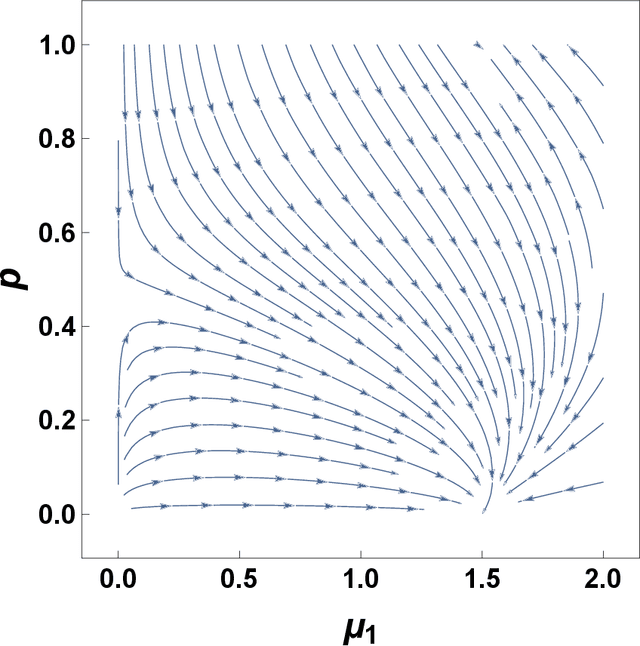
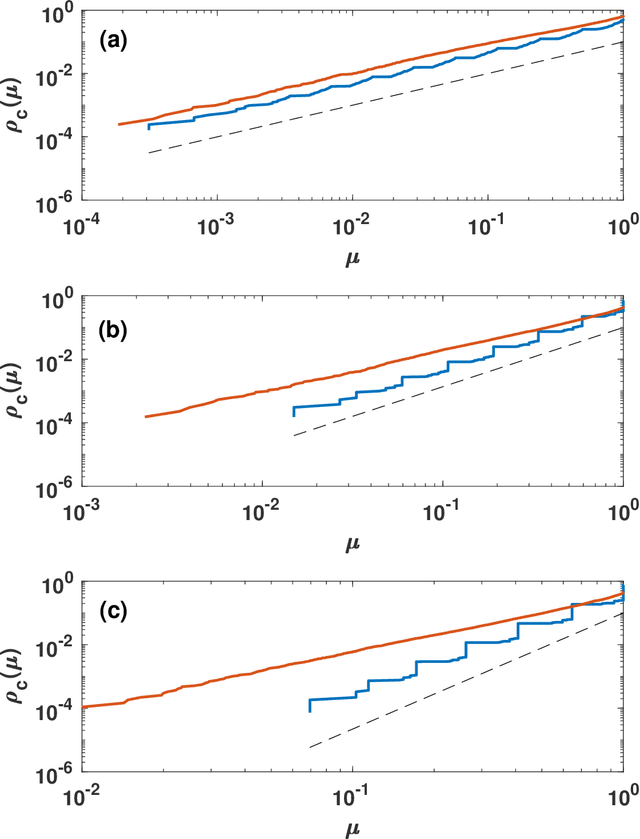
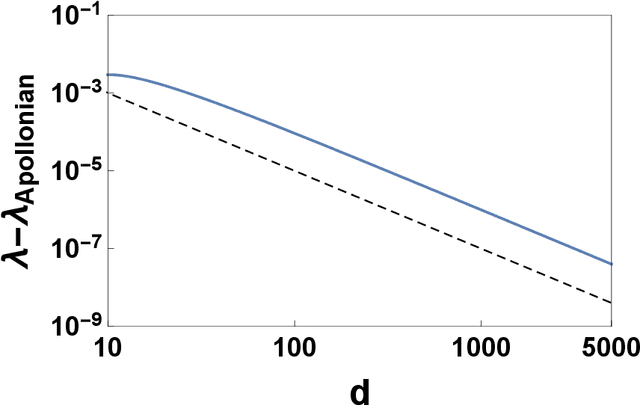
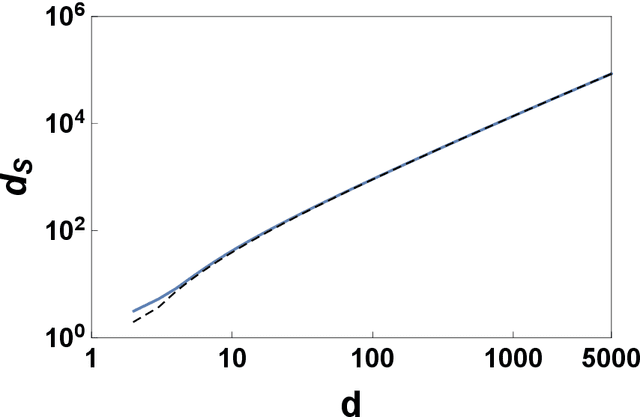
Simplicial complexes are increasingly used to study complex system structure and dynamics including diffusion, synchronization and epidemic spreading. The spectral dimension of the graph Laplacian is known to determine the diffusion properties at long time scales. Using the renormalization group here we calculate the spectral dimension of the graph Laplacian of two classes of non-amenable $d$ dimensional simplicial complexes: the Apollonian networks and the pseudo-fractal networks. We analyse the scaling of the spectral dimension with the topological dimension $d$ for $d\to \infty$ and we point out that randomness such as the one present in Network Geometry with Flavor can diminish the value of the spectral dimension of these structures.
* (30 pages, 5 figures)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge