Latent Geometry Inspired Graph Dissimilarities Enhance Affinity Propagation Community Detection in Complex Networks
Paper and Code
Aug 29, 2018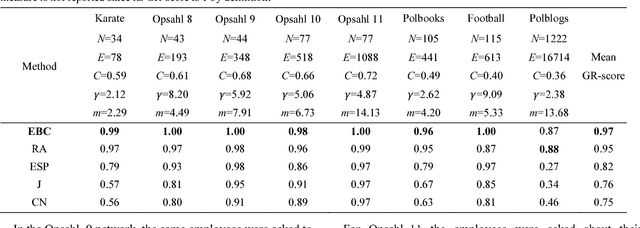
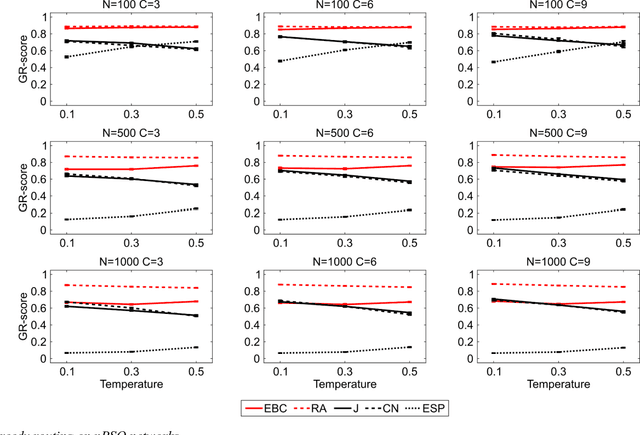


Affinity propagation is one of the most effective unsupervised pattern recognition algorithms for data clustering in high-dimensional feature space. However, the numerous attempts to test its performance for community detection in complex networks have been attaining results very far from the state of the art methods such as Infomap and Louvain. Yet, all these studies agreed that the crucial problem is to convert the unweighted network topology in a 'smart-enough' node dissimilarity matrix that is able to properly address the message passing procedure behind affinity propagation clustering. Here we introduce a conceptual innovation and we discuss how to leverage network latent geometry notions in order to design dissimilarity matrices for affinity propagation community detection. Our results demonstrate that the latent geometry inspired dissimilarity measures we design bring affinity propagation to equal or outperform current state of the art methods for community detection. These findings are solidly proven considering both synthetic 'realistic' networks (with known ground-truth communities) and real networks (with community metadata), even when the data structure is corrupted by noise artificially induced by missing or spurious connectivity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge