Interpreting Temporal Graph Neural Networks with Koopman Theory

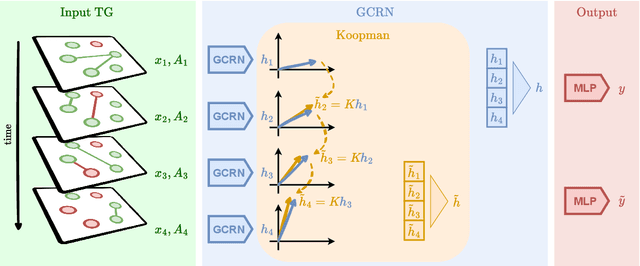
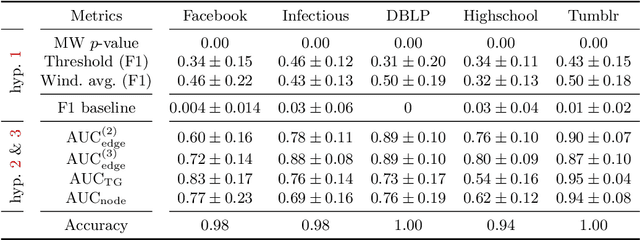
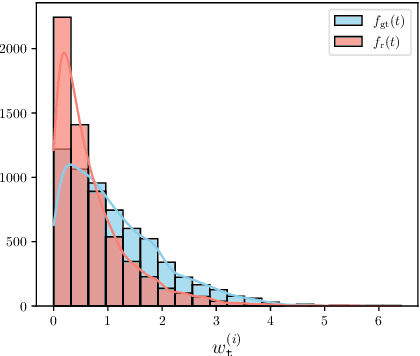
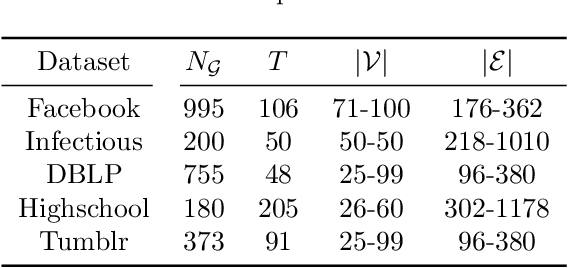
Spatiotemporal graph neural networks (STGNNs) have shown promising results in many domains, from forecasting to epidemiology. However, understanding the dynamics learned by these models and explaining their behaviour is significantly more complex than for models dealing with static data. Inspired by Koopman theory, which allows a simpler description of intricate, nonlinear dynamical systems, we introduce an explainability approach for temporal graphs. We present two methods to interpret the STGNN's decision process and identify the most relevant spatial and temporal patterns in the input for the task at hand. The first relies on dynamic mode decomposition (DMD), a Koopman-inspired dimensionality reduction method. The second relies on sparse identification of nonlinear dynamics (SINDy), a popular method for discovering governing equations, which we use for the first time as a general tool for explainability. We show how our methods can correctly identify interpretable features such as infection times and infected nodes in the context of dissemination processes.

Probabilistic load forecasting with Reservoir Computing

Some applications of deep learning require not only to provide accurate results but also to quantify the amount of confidence in their prediction. The management of an electric power grid is one of these cases: to avoid risky scenarios, decision-makers need both precise and reliable forecasts of, for example, power loads. For this reason, point forecasts are not enough hence it is necessary to adopt methods that provide an uncertainty quantification. This work focuses on reservoir computing as the core time series forecasting method, due to its computational efficiency and effectiveness in predicting time series. While the RC literature mostly focused on point forecasting, this work explores the compatibility of some popular uncertainty quantification methods with the reservoir setting. Both Bayesian and deterministic approaches to uncertainty assessment are evaluated and compared in terms of their prediction accuracy, computational resource efficiency and reliability of the estimated uncertainty, based on a set of carefully chosen performance metrics.

Combining Stochastic Explainers and Subgraph Neural Networks can Increase Expressivity and Interpretability

Subgraph-enhanced graph neural networks (SGNN) can increase the expressive power of the standard message-passing framework. This model family represents each graph as a collection of subgraphs, generally extracted by random sampling or with hand-crafted heuristics. Our key observation is that by selecting "meaningful" subgraphs, besides improving the expressivity of a GNN, it is also possible to obtain interpretable results. For this purpose, we introduce a novel framework that jointly predicts the class of the graph and a set of explanatory sparse subgraphs, which can be analyzed to understand the decision process of the classifier. We compare the performance of our framework against standard subgraph extraction policies, like random node/edge deletion strategies. The subgraphs produced by our framework allow to achieve comparable performance in terms of accuracy, with the additional benefit of providing explanations.

Explainability in subgraphs-enhanced Graph Neural Networks

Recently, subgraphs-enhanced Graph Neural Networks (SGNNs) have been introduced to enhance the expressive power of Graph Neural Networks (GNNs), which was proved to be not higher than the 1-dimensional Weisfeiler-Leman isomorphism test. The new paradigm suggests using subgraphs extracted from the input graph to improve the model's expressiveness, but the additional complexity exacerbates an already challenging problem in GNNs: explaining their predictions. In this work, we adapt PGExplainer, one of the most recent explainers for GNNs, to SGNNs. The proposed explainer accounts for the contribution of all the different subgraphs and can produce a meaningful explanation that humans can interpret. The experiments that we performed both on real and synthetic datasets show that our framework is successful in explaining the decision process of an SGNN on graph classification tasks.