Clustering with Total Variation Graph Neural Networks

Graph Neural Networks (GNNs) are deep learning models designed to process attributed graphs. GNNs can compute cluster assignments accounting both for the vertex features and for the graph topology. Existing GNNs for clustering are trained by optimizing an unsupervised minimum cut objective, which is approximated by a Spectral Clustering (SC) relaxation. SC offers a closed-form solution that, however, is not particularly useful for a GNN trained with gradient descent. Additionally, the SC relaxation is loose and yields overly smooth cluster assignments, which do not separate well the samples. We propose a GNN model that optimizes a tighter relaxation of the minimum cut based on graph total variation (GTV). Our model has two core components: i) a message-passing layer that minimizes the $\ell_1$ distance in the features of adjacent vertices, which is key to achieving sharp cluster transitions; ii) a loss function that minimizes the GTV in the cluster assignments while ensuring balanced partitions. By optimizing the proposed loss, our model can be self-trained to perform clustering. In addition, our clustering procedure can be used to implement graph pooling in deep GNN architectures for graph classification. Experiments show that our model outperforms other GNN-based approaches for clustering and graph pooling.

Power Flow Balancing with Decentralized Graph Neural Networks

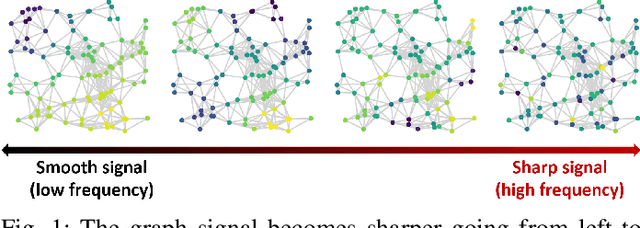
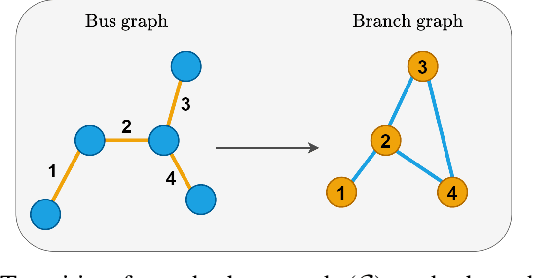
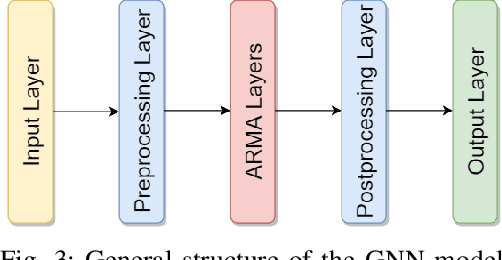
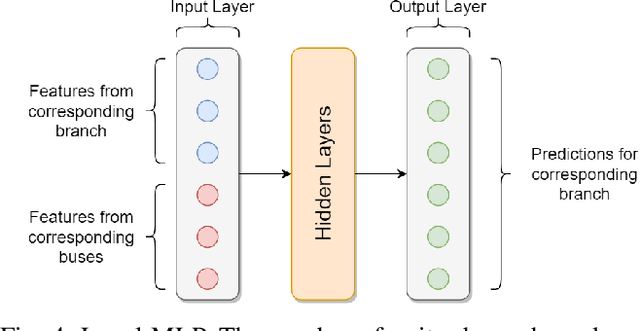
We propose an end-to-end framework based on a Graph Neural Network (GNN) to balance the power flows in a generic grid. The optimization is framed as a supervised vertex regression task, where the GNN is trained to predict the current and power injections at each grid branch that yield a power flow balance. By representing the power grid as a line graph with branches as vertices, we can train a GNN that is more accurate and robust to changes in the underlying topology. In addition, by using specialized GNN layers, we are able to build a very deep architecture that accounts for large neighborhoods on the graph, while implementing only localized operations. We perform three different experiments to evaluate: i) the benefits of using localized rather than global operations and the tendency to oversmooth when using deep GNN models; ii) the resilience to perturbations in the graph topology; and iii) the capability to train the model simultaneously on multiple grid topologies and the consequential improvement in generalization to new, unseen grids. The proposed framework is efficient and, compared to other solvers based on deep learning, is robust to perturbations not only to the physical quantities on the grid components, but also to the topology.