Anti-Symmetric DGN: a stable architecture for Deep Graph Networks
Paper and Code
Oct 18, 2022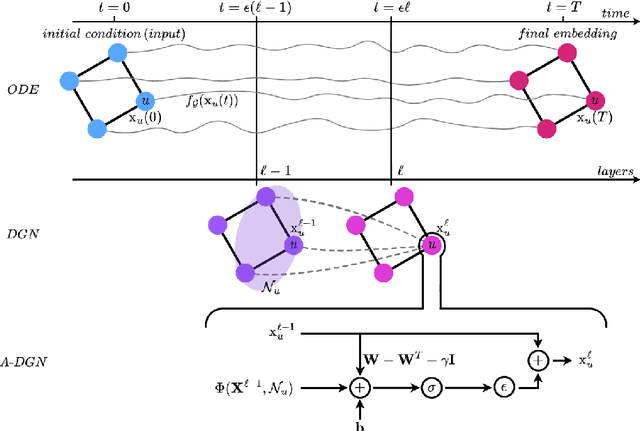

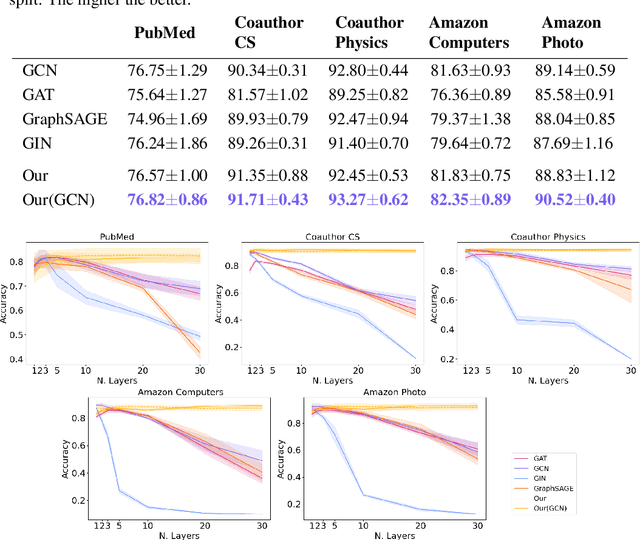

Deep Graph Networks (DGNs) currently dominate the research landscape of learning from graphs, due to their efficiency and ability to implement an adaptive message-passing scheme between the nodes. However, DGNs are typically limited in their ability to propagate and preserve long-term dependencies between nodes, \ie they suffer from the over-squashing phenomena. This reduces their effectiveness, since predictive problems may require to capture interactions at different, and possibly large, radii in order to be effectively solved. In this work, we present Anti-Symmetric Deep Graph Networks (A-DGNs), a framework for stable and non-dissipative DGN design, conceived through the lens of ordinary differential equations. We give theoretical proof that our method is stable and non-dissipative, leading to two key results: long-range information between nodes is preserved, and no gradient vanishing or explosion occurs in training. We empirically validate the proposed approach on several graph benchmarks, showing that A-DGN yields to improved performance and enables to learn effectively even when dozens of layers are used.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge