Learning Augmentation Distributions using Transformed Risk Minimization

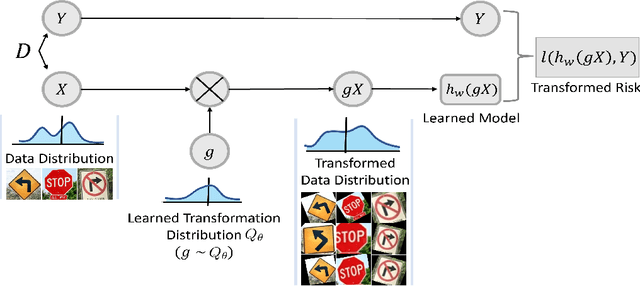
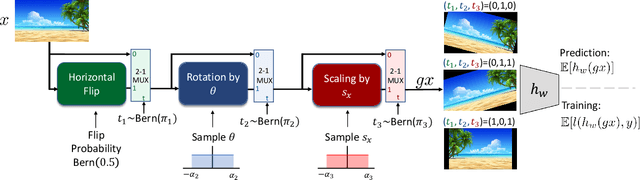
Adapting to the structure of data distributions (such as symmetry and transformation invariances) is an important challenge in machine learning. Invariances can be built into the learning process by architecture design, or by augmenting the dataset. Both require a priori knowledge about the exact nature of the symmetries. Absent this knowledge, practitioners resort to expensive and time-consuming tuning. To address this problem, we propose a new approach to learn distributions of augmentation transforms, in a new \emph{Transformed Risk Minimization} (TRM) framework. In addition to predictive models, we also optimize over transformations chosen from a hypothesis space. As an algorithmic framework, our TRM method is (1) efficient (jointly learns augmentations and models in a \emph{single training loop}), (2) modular (works with \emph{any} training algorithm), and (3) general (handles \emph{both discrete and continuous} augmentations). We theoretically compare TRM with standard risk minimization, and give a PAC-Bayes upper bound on its generalization error. We propose to optimize this bound over a rich augmentation space via a new parametrization over compositions of blocks, leading to the new \emph{Stochastic Compositional Augmentation Learning} (SCALE) algorithm. We compare SCALE experimentally with prior methods (Fast AutoAugment and Augerino) on CIFAR10/100, SVHN . Additionally, we show that SCALE can correctly learn certain symmetries in the data distribution (recovering rotations on rotated MNIST) and can also improve calibration of the learned model.