Conformal Prediction Intervals with Temporal Dependence
Paper and Code
May 26, 2022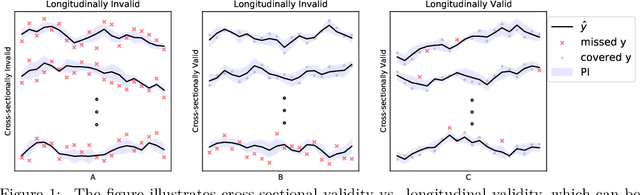


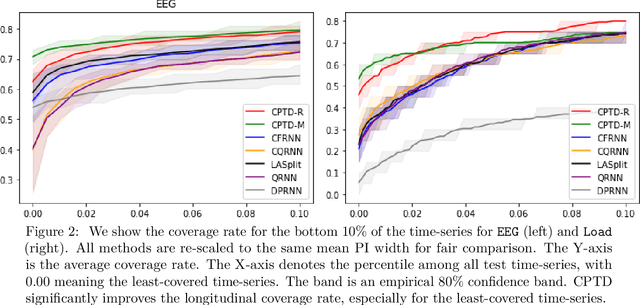
Cross-sectional prediction is common in many domains such as healthcare, including forecasting tasks using electronic health records, where different patients form a cross-section. We focus on the task of constructing valid prediction intervals (PIs) in time-series regression with a cross-section. A prediction interval is considered valid if it covers the true response with (a pre-specified) high probability. We first distinguish between two notions of validity in such a setting: cross-sectional and longitudinal. Cross-sectional validity is concerned with validity across the cross-section of the time series data, while longitudinal validity accounts for the temporal dimension. Coverage guarantees along both these dimensions are ideally desirable; however, we show that distribution-free longitudinal validity is theoretically impossible. Despite this limitation, we propose Conformal Prediction with Temporal Dependence (CPTD), a procedure which is able to maintain strict cross-sectional validity while improving longitudinal coverage. CPTD is post-hoc and light-weight, and can easily be used in conjunction with any prediction model as long as a calibration set is available. We focus on neural networks due to their ability to model complicated data such as diagnosis codes for time-series regression, and perform extensive experimental validation to verify the efficacy of our approach. We find that CPTD outperforms baselines on a variety of datasets by improving longitudinal coverage and often providing more efficient (narrower) PIs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge