Classification based on Topological Data Analysis
Paper and Code
Feb 07, 2021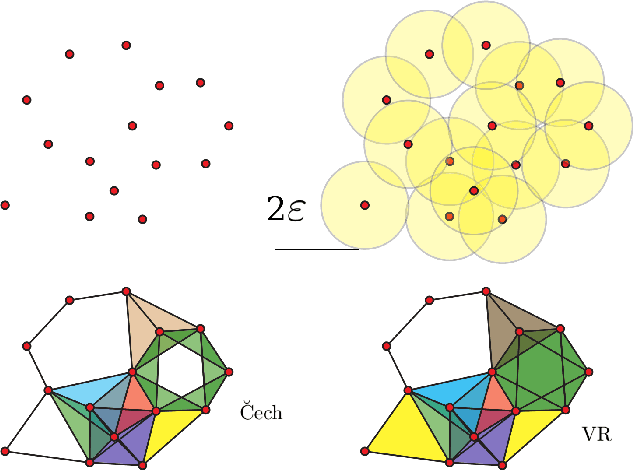
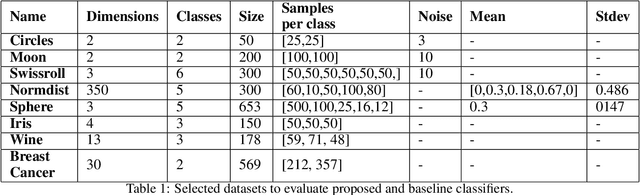
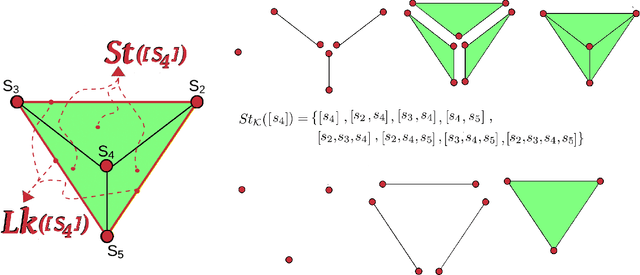

Topological Data Analysis (TDA) is an emergent field that aims to discover topological information hidden in a dataset. TDA tools have been commonly used to create filters and topological descriptors to improve Machine Learning (ML) methods. This paper proposes an algorithm that applies TDA directly to multi-class classification problems, even imbalanced datasets, without any further ML stage. The proposed algorithm built a filtered simplicial complex on the dataset. Persistent homology is then applied to guide choosing a sub-complex where unlabeled points obtain the label with most votes from labeled neighboring points. To assess the proposed method, 8 datasets were selected with several degrees of class entanglement, variability on the samples per class, and dimensionality. On average, the proposed TDABC method was capable of overcoming baseline classifiers (wk-NN and k-NN) in each of the computed metrics, especially on classifying entangled and minority classes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge