Enrique Alvarado
$G$-Mapper: Learning a Cover in the Mapper Construction
Sep 12, 2023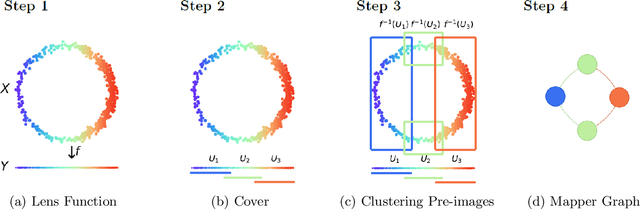

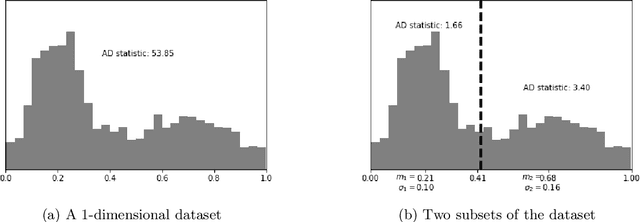
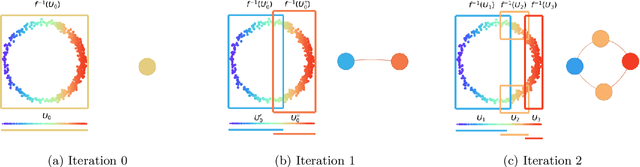
Abstract:The Mapper algorithm is a visualization technique in topological data analysis (TDA) that outputs a graph reflecting the structure of a given dataset. The Mapper algorithm requires tuning several parameters in order to generate a "nice" Mapper graph. The paper focuses on selecting the cover parameter. We present an algorithm that optimizes the cover of a Mapper graph by splitting a cover repeatedly according to a statistical test for normality. Our algorithm is based on $G$-means clustering which searches for the optimal number of clusters in $k$-means by conducting iteratively the Anderson-Darling test. Our splitting procedure employs a Gaussian mixture model in order to choose carefully the cover based on the distribution of a given data. Experiments for synthetic and real-world datasets demonstrate that our algorithm generates covers so that the Mapper graphs retain the essence of the datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge