$G$-Mapper: Learning a Cover in the Mapper Construction

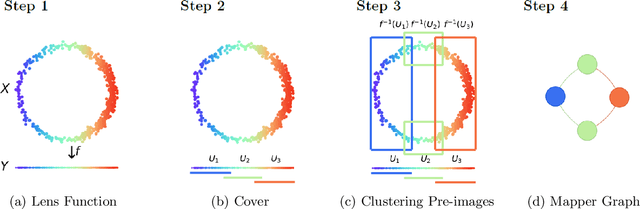
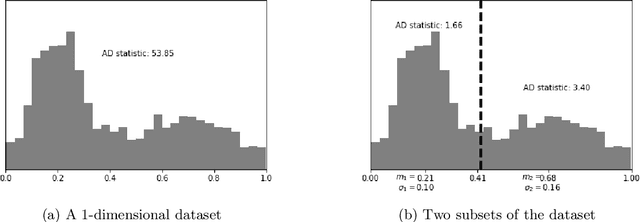
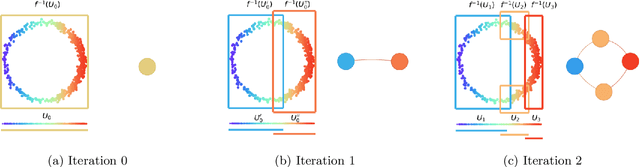
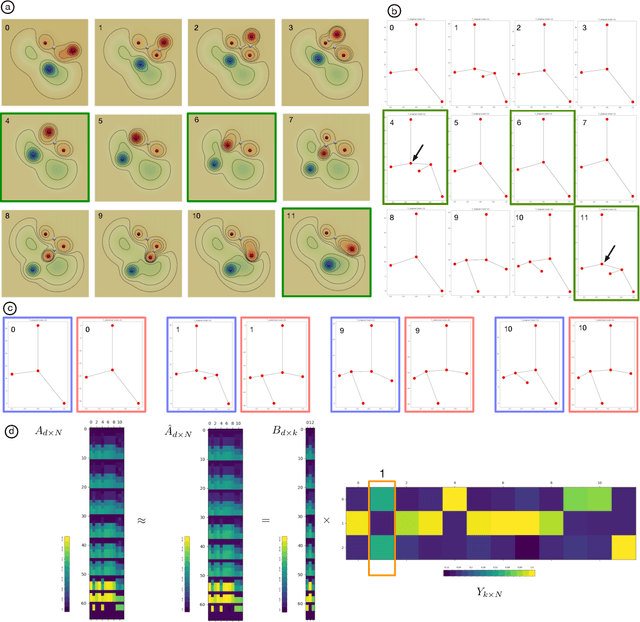
The Mapper algorithm is a visualization technique in topological data analysis (TDA) that outputs a graph reflecting the structure of a given dataset. The Mapper algorithm requires tuning several parameters in order to generate a "nice" Mapper graph. The paper focuses on selecting the cover parameter. We present an algorithm that optimizes the cover of a Mapper graph by splitting a cover repeatedly according to a statistical test for normality. Our algorithm is based on $G$-means clustering which searches for the optimal number of clusters in $k$-means by conducting iteratively the Anderson-Darling test. Our splitting procedure employs a Gaussian mixture model in order to choose carefully the cover based on the distribution of a given data. Experiments for synthetic and real-world datasets demonstrate that our algorithm generates covers so that the Mapper graphs retain the essence of the datasets.

Sketching Merge Trees

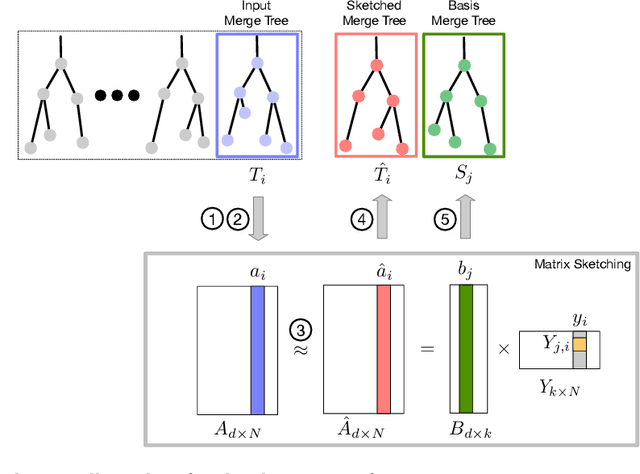
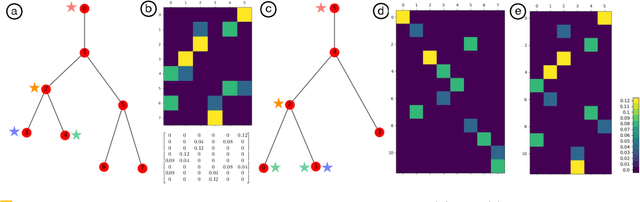
Merge trees are a type of topological descriptors that record the connectivity among the sublevel sets of scalar fields. In this paper, we are interested in sketching a set of merge trees. That is, given a set T of merge trees, we would like to find a basis set S such that each tree in T can be approximately reconstructed from a linear combination of merge trees in S. A set of high-dimensional vectors can be sketched via matrix sketching techniques such as principal component analysis and column subset selection. However, up until now, topological descriptors such as merge trees have not been known to be sketchable. We develop a framework for sketching a set of merge trees that combines the Gromov-Wasserstein framework of Chowdhury and Needham with techniques from matrix sketching. We demonstrate the applications of our framework in sketching merge trees that arise from data ensembles in scientific simulations.

TopoAct: Exploring the Shape of Activations in Deep Learning

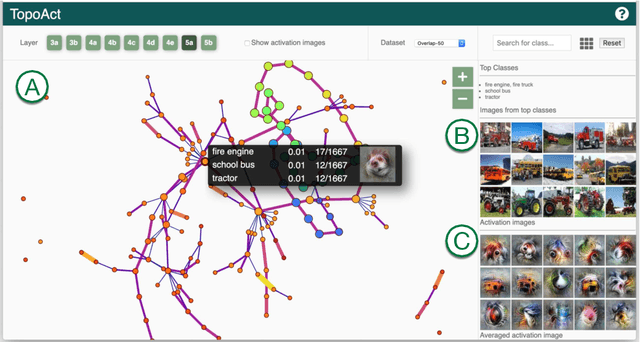
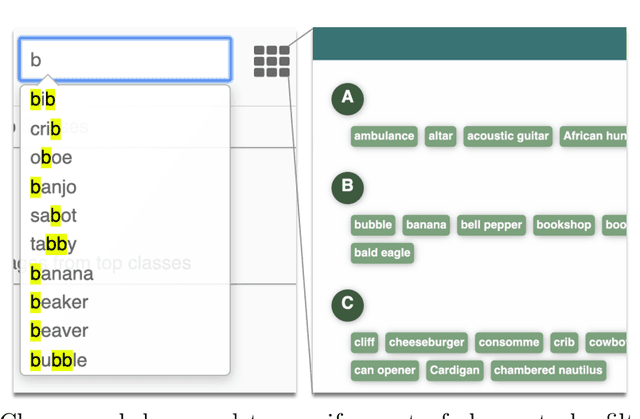
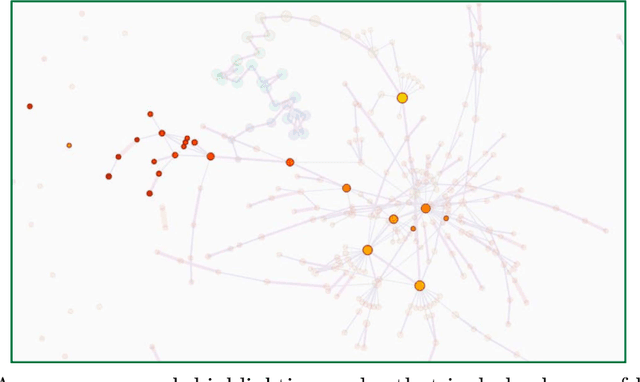
Deep neural networks such as GoogLeNet and ResNet have achieved superhuman performance in tasks like image classification. To understand how such superior performance is achieved, we can probe a trained deep neural network by studying neuron activations, that is, combinations of neuron firings, at any layer of the network in response to a particular input. With a large set of input images, we aim to obtain a global view of what neurons detect by studying their activations. We ask the following questions: What is the shape of the space of activations? That is, what is the organizational principle behind neuron activations, and how are the activations related within a layer and across layers? Applying tools from topological data analysis, we present TopoAct, a visual exploration system used to study topological summaries of activation vectors for a single layer as well as the evolution of such summaries across multiple layers. We present visual exploration scenarios using TopoAct that provide valuable insights towards learned representations of an image classifier.