Machines and Mathematical Mutations: Using GNNs to Characterize Quiver Mutation Classes

Machine learning is becoming an increasingly valuable tool in mathematics, enabling one to identify subtle patterns across collections of examples so vast that they would be impossible for a single researcher to feasibly review and analyze. In this work, we use graph neural networks to investigate quiver mutation -- an operation that transforms one quiver (or directed multigraph) into another -- which is central to the theory of cluster algebras with deep connections to geometry, topology, and physics. In the study of cluster algebras, the question of mutation equivalence is of fundamental concern: given two quivers, can one efficiently determine if one quiver can be transformed into the other through a sequence of mutations? Currently, this question has only been resolved in specific cases. In this paper, we use graph neural networks and AI explainability techniques to discover mutation equivalence criteria for the previously unknown case of quivers of type $\tilde{D}_n$. Along the way, we also show that even without explicit training to do so, our model captures structure within its hidden representation that allows us to reconstruct known criteria from type $D_n$, adding to the growing evidence that modern machine learning models are capable of learning abstract and general rules from mathematical data.

Faster Fuzzing: Reinitialization with Deep Neural Models

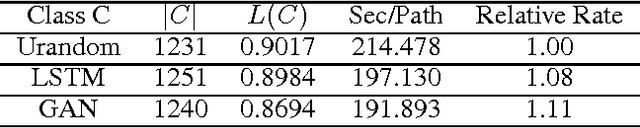
We improve the performance of the American Fuzzy Lop (AFL) fuzz testing framework by using Generative Adversarial Network (GAN) models to reinitialize the system with novel seed files. We assess performance based on the temporal rate at which we produce novel and unseen code paths. We compare this approach to seed file generation from a random draw of bytes observed in the training seed files. The code path lengths and variations were not sufficiently diverse to fully replace AFL input generation. However, augmenting native AFL with these additional code paths demonstrated improvements over AFL alone. Specifically, experiments showed the GAN was faster and more effective than the LSTM and out-performed a random augmentation strategy, as measured by the number of unique code paths discovered. GAN helps AFL discover 14.23% more code paths than the random strategy in the same amount of CPU time, finds 6.16% more unique code paths, and finds paths that are on average 13.84% longer. Using GAN shows promise as a reinitialization strategy for AFL to help the fuzzer exercise deep paths in software.