Diffusion Models Through a Global Lens: Are They Culturally Inclusive?

Text-to-image diffusion models have recently enabled the creation of visually compelling, detailed images from textual prompts. However, their ability to accurately represent various cultural nuances remains an open question. In our work, we introduce CultDiff benchmark, evaluating state-of-the-art diffusion models whether they can generate culturally specific images spanning ten countries. We show that these models often fail to generate cultural artifacts in architecture, clothing, and food, especially for underrepresented country regions, by conducting a fine-grained analysis of different similarity aspects, revealing significant disparities in cultural relevance, description fidelity, and realism compared to real-world reference images. With the collected human evaluations, we develop a neural-based image-image similarity metric, namely, CultDiff-S, to predict human judgment on real and generated images with cultural artifacts. Our work highlights the need for more inclusive generative AI systems and equitable dataset representation over a wide range of cultures.

Revisiting Random Walks for Learning on Graphs

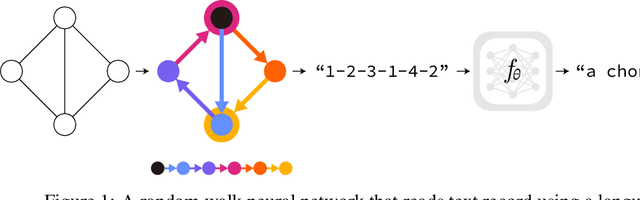
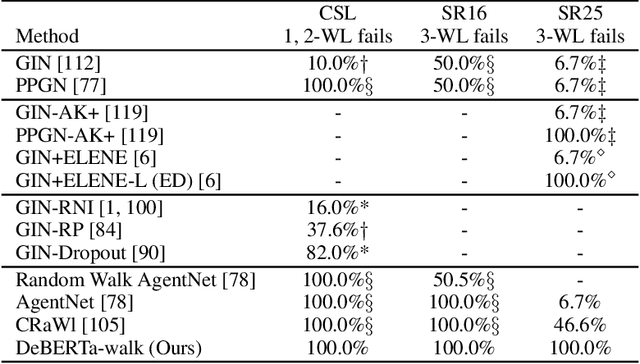
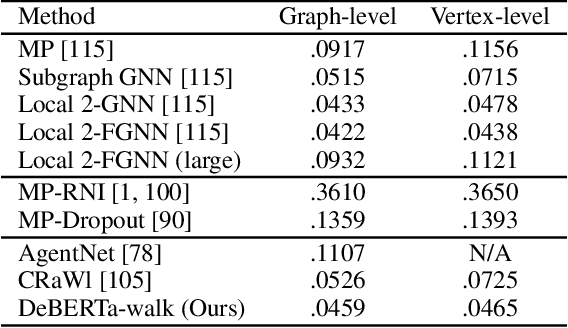
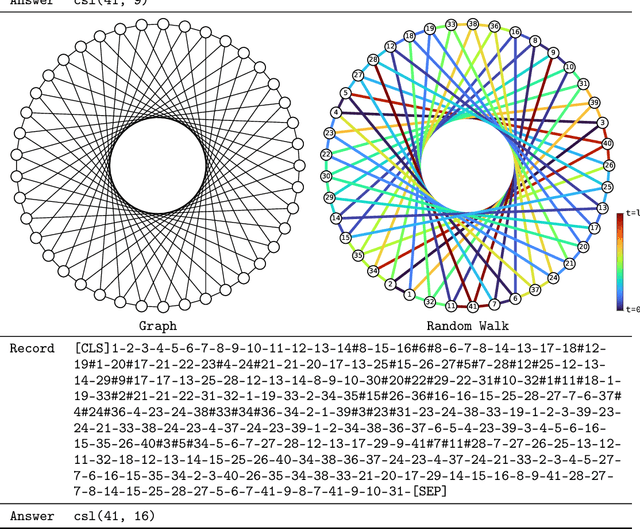
We revisit a simple idea for machine learning on graphs, where a random walk on a graph produces a machine-readable record, and this record is processed by a deep neural network to directly make vertex-level or graph-level predictions. We refer to these stochastic machines as random walk neural networks, and show that we can design them to be isomorphism invariant while capable of universal approximation of graph functions in probability. A useful finding is that almost any kind of record of random walk guarantees probabilistic invariance as long as the vertices are anonymized. This enables us to record random walks in plain text and adopt a language model to read these text records to solve graph tasks. We further establish a parallelism to message passing neural networks using tools from Markov chain theory, and show that over-smoothing in message passing is alleviated by construction in random walk neural networks, while over-squashing manifests as probabilistic under-reaching. We show that random walk neural networks based on pre-trained language models can solve several hard problems on graphs, such as separating strongly regular graphs where the 3-WL test fails, counting substructures, and transductive classification on arXiv citation network without training. Code is available at https://github.com/jw9730/random-walk.

Learning Probabilistic Symmetrization for Architecture Agnostic Equivariance

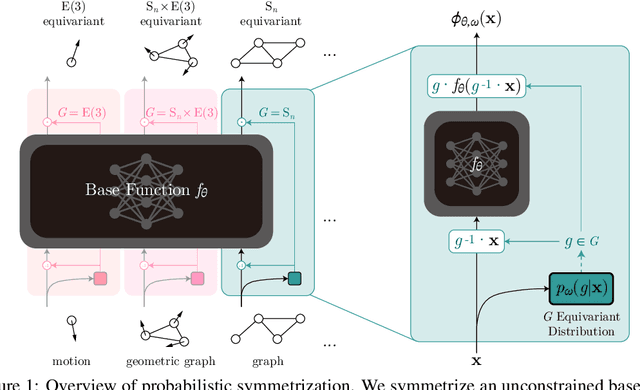
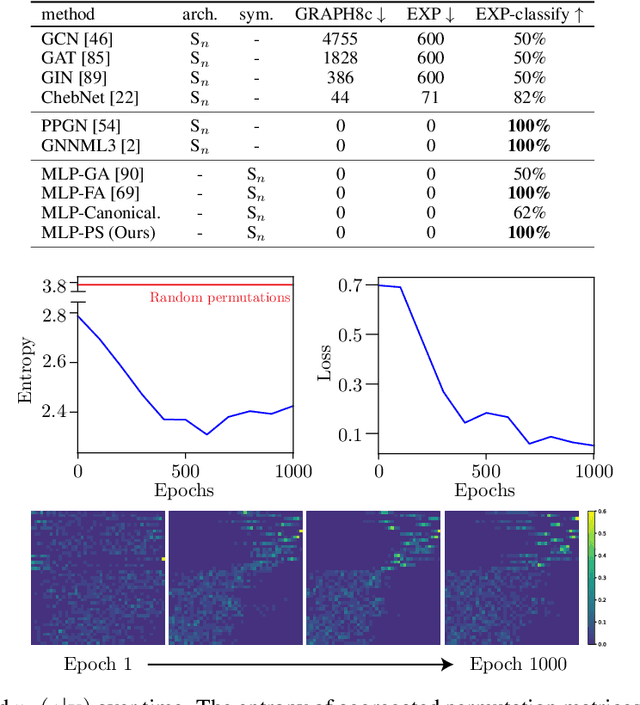
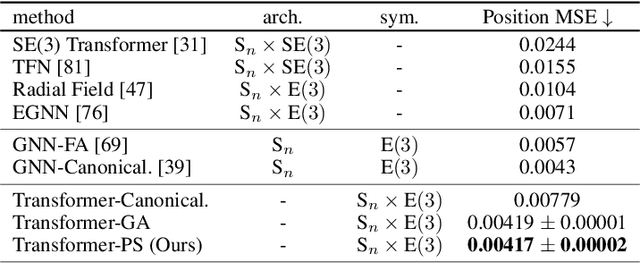
We present a novel framework to overcome the limitations of equivariant architectures in learning functions with group symmetries. In contrary to equivariant architectures, we use an arbitrary base model (such as an MLP or a transformer) and symmetrize it to be equivariant to the given group by employing a small equivariant network that parameterizes the probabilistic distribution underlying the symmetrization. The distribution is end-to-end trained with the base model which can maximize performance while reducing sample complexity of symmetrization. We show that this approach ensures not only equivariance to given group but also universal approximation capability in expectation. We implement our method on a simple patch-based transformer that can be initialized from pretrained vision transformers, and test it for a wide range of symmetry groups including permutation and Euclidean groups and their combinations. Empirical tests show competitive results against tailored equivariant architectures, suggesting the potential for learning equivariant functions for diverse groups using a non-equivariant universal base architecture. We further show evidence of enhanced learning in symmetric modalities, like graphs, when pretrained from non-symmetric modalities, like vision. Our implementation will be open-sourced at https://github.com/jw9730/lps.