UniSemAlign: Text-Prototype Alignment with a Foundation Encoder for Semi-Supervised Histopathology Segmentation

Semi-supervised semantic segmentation in computational pathology remains challenging due to scarce pixel-level annotations and unreliable pseudo-label supervision. We propose UniSemAlign, a dual-modal semantic alignment framework that enhances visual segmentation by injecting explicit class-level structure into pixel-wise learning. Built upon a pathology-pretrained Transformer encoder, UniSemAlign introduces complementary prototype-level and text-level alignment branches in a shared embedding space, providing structured guidance that reduces class ambiguity and stabilizes pseudo-label refinement. The aligned representations are fused with visual predictions to generate more reliable supervision for unlabeled histopathology images. The framework is trained end-to-end with supervised segmentation, cross-view consistency, and cross-modal alignment objectives. Extensive experiments on the GlaS and CRAG datasets demonstrate that UniSemAlign substantially outperforms recent semi-supervised baselines under limited supervision, achieving Dice improvements of up to 2.6% on GlaS and 8.6% on CRAG with only 10% labeled data, and strong improvements at 20% supervision. Code is available at: https://github.com/thailevann/UniSemAlign

High-dimensional Many-to-many-to-many Mediation Analysis

We study high-dimensional mediation analysis in which exposures, mediators, and outcomes are all multivariate, and both exposures and mediators may be high-dimensional. We formalize this as a many (exposures)-to-many (mediators)-to-many (outcomes) (MMM) mediation analysis problem. Methodologically, MMM mediation analysis simultaneously performs variable selection for high-dimensional exposures and mediators, estimates the indirect effect matrix (i.e., the coefficient matrices linking exposure-to-mediator and mediator-to-outcome pathways), and enables prediction of multivariate outcomes. Theoretically, we show that the estimated indirect effect matrices are consistent and element-wise asymptotically normal, and we derive error bounds for the estimators. To evaluate the efficacy of the MMM mediation framework, we first investigate its finite-sample performance, including convergence properties, the behavior of the asymptotic approximations, and robustness to noise, via simulation studies. We then apply MMM mediation analysis to data from the Alzheimer's Disease Neuroimaging Initiative to study how cortical thickness of 202 brain regions may mediate the effects of 688 genome-wide significant single nucleotide polymorphisms (SNPs) (selected from approximately 1.5 million SNPs) on eleven cognitive-behavioral and diagnostic outcomes. The MMM mediation framework identifies biologically interpretable, many-to-many-to-many genetic-neural-cognitive pathways and improves downstream out-of-sample classification and prediction performance. Taken together, our results demonstrate the potential of MMM mediation analysis and highlight the value of statistical methodology for investigating complex, high-dimensional multi-layer pathways in science. The MMM package is available at https://github.com/THELabTop/MMM-Mediation.

Learning Symmetrization for Equivariance with Orbit Distance Minimization

We present a general framework for symmetrizing an arbitrary neural-network architecture and making it equivariant with respect to a given group. We build upon the proposals of Kim et al. (2023); Kaba et al. (2023) for symmetrization, and improve them by replacing their conversion of neural features into group representations, with an optimization whose loss intuitively measures the distance between group orbits. This change makes our approach applicable to a broader range of matrix groups, such as the Lorentz group O(1, 3), than these two proposals. We experimentally show our method's competitiveness on the SO(2) image classification task, and also its increased generality on the task with O(1, 3). Our implementation will be made accessible at https://github.com/tiendatnguyen-vision/Orbit-symmetrize.

Learning Probabilistic Symmetrization for Architecture Agnostic Equivariance

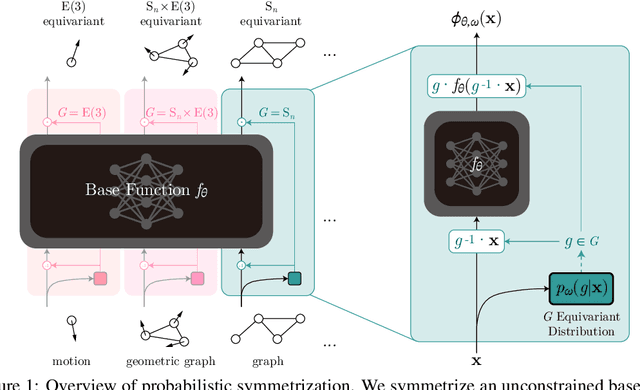
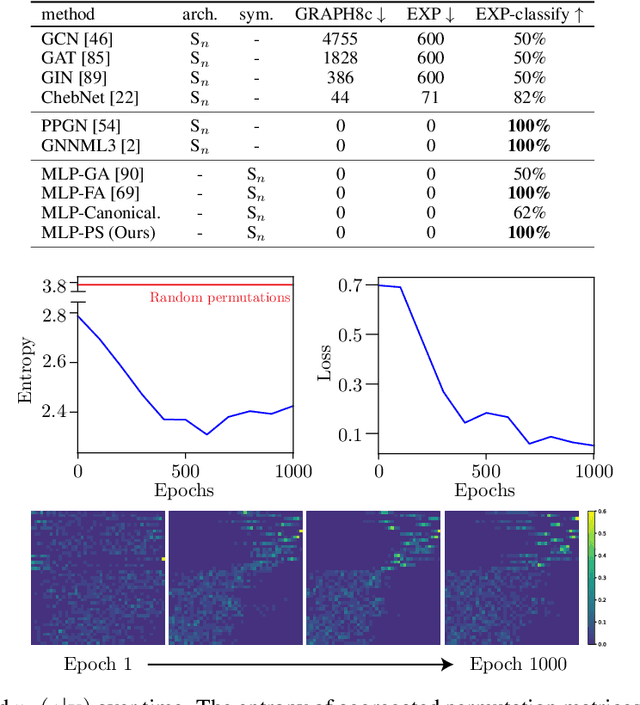
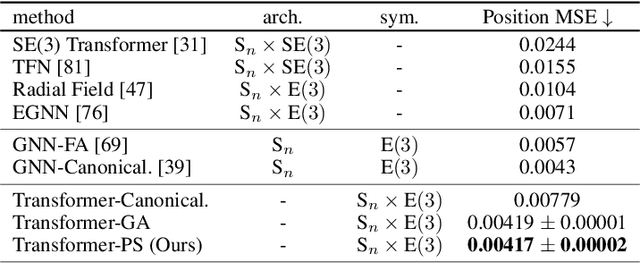
We present a novel framework to overcome the limitations of equivariant architectures in learning functions with group symmetries. In contrary to equivariant architectures, we use an arbitrary base model (such as an MLP or a transformer) and symmetrize it to be equivariant to the given group by employing a small equivariant network that parameterizes the probabilistic distribution underlying the symmetrization. The distribution is end-to-end trained with the base model which can maximize performance while reducing sample complexity of symmetrization. We show that this approach ensures not only equivariance to given group but also universal approximation capability in expectation. We implement our method on a simple patch-based transformer that can be initialized from pretrained vision transformers, and test it for a wide range of symmetry groups including permutation and Euclidean groups and their combinations. Empirical tests show competitive results against tailored equivariant architectures, suggesting the potential for learning equivariant functions for diverse groups using a non-equivariant universal base architecture. We further show evidence of enhanced learning in symmetric modalities, like graphs, when pretrained from non-symmetric modalities, like vision. Our implementation will be open-sourced at https://github.com/jw9730/lps.

Pure Transformers are Powerful Graph Learners

We show that standard Transformers without graph-specific modifications can lead to promising results in graph learning both in theory and practice. Given a graph, we simply treat all nodes and edges as independent tokens, augment them with token embeddings, and feed them to a Transformer. With an appropriate choice of token embeddings, we prove that this approach is theoretically at least as expressive as an invariant graph network (2-IGN) composed of equivariant linear layers, which is already more expressive than all message-passing Graph Neural Networks (GNN). When trained on a large-scale graph dataset (PCQM4Mv2), our method coined Tokenized Graph Transformer (TokenGT) achieves significantly better results compared to GNN baselines and competitive results compared to Transformer variants with sophisticated graph-specific inductive bias. Our implementation is available at https://github.com/jw9730/tokengt.