Nonlinear Sheaf Diffusion in Graph Neural Networks
Paper and Code
Mar 01, 2024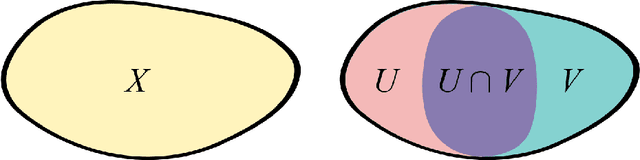
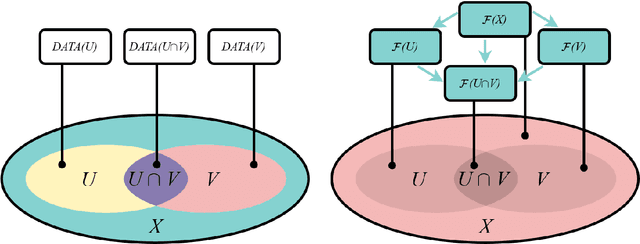
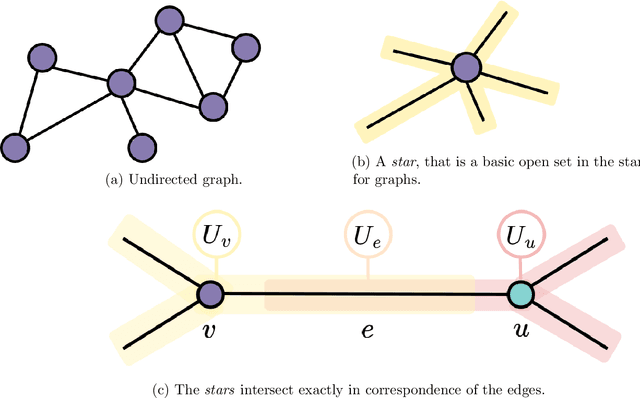
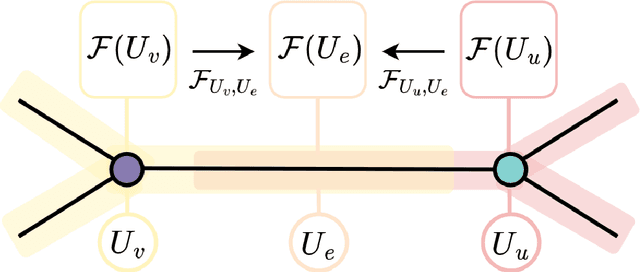
This work focuses on exploring the potential benefits of introducing a nonlinear Laplacian in Sheaf Neural Networks for graph-related tasks. The primary aim is to understand the impact of such nonlinearity on diffusion dynamics, signal propagation, and performance of neural network architectures in discrete-time settings. The study primarily emphasizes experimental analysis, using real-world and synthetic datasets to validate the practical effectiveness of different versions of the model. This approach shifts the focus from an initial theoretical exploration to demonstrating the practical utility of the proposed model.
* Thesis for Master's degree in Artificial Intelligence Systems
(University of Trento), 65 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge