ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

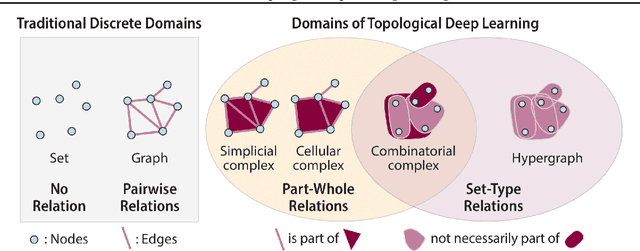
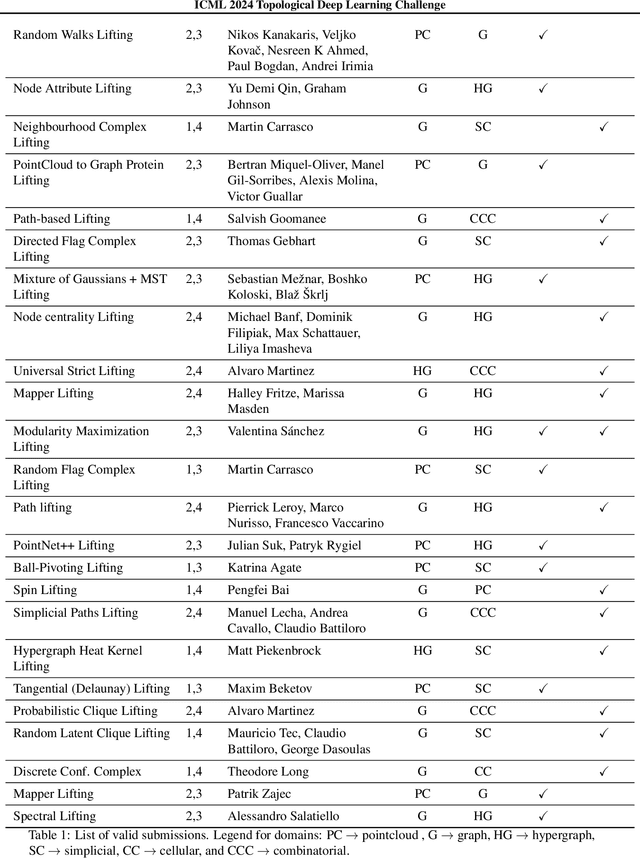
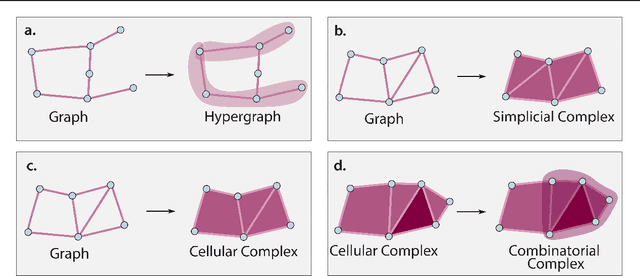
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

E(n) Equivariant Message Passing Cellular Networks

This paper introduces E(n) Equivariant Message Passing Cellular Networks (EMPCNs), an extension of E(n) Equivariant Graph Neural Networks to CW-complexes. Our approach addresses two aspects of geometric message passing networks: 1) enhancing their expressiveness by incorporating arbitrary cells, and 2) achieving this in a computationally efficient way with a decoupled EMPCNs technique. We demonstrate that EMPCNs achieve close to state-of-the-art performance on multiple tasks without the need for steerability, including many-body predictions and motion capture. Moreover, ablation studies confirm that decoupled EMPCNs exhibit stronger generalization capabilities than their non-topologically informed counterparts. These findings show that EMPCNs can be used as a scalable and expressive framework for higher-order message passing in geometric and topological graphs