ActUp: Analyzing and Consolidating tSNE and UMAP

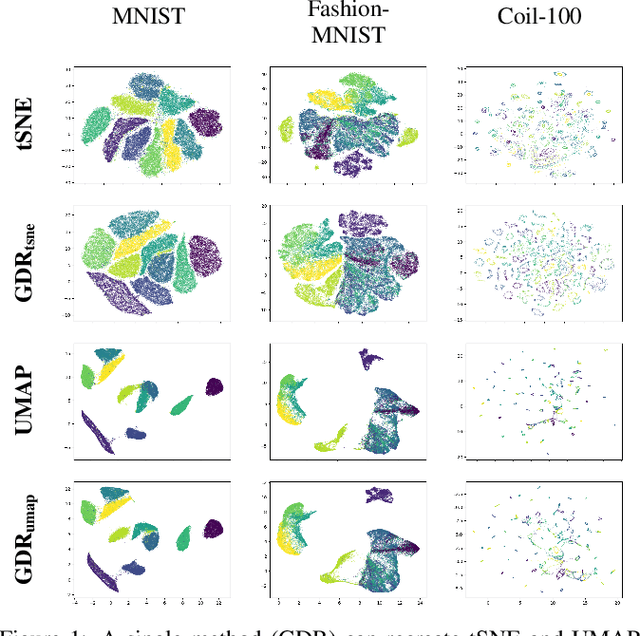
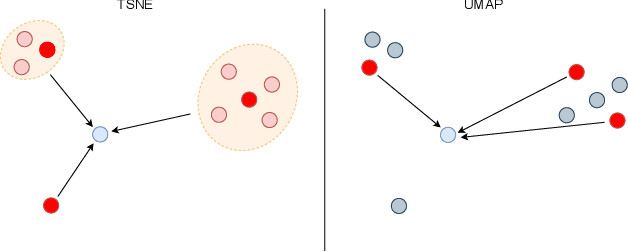
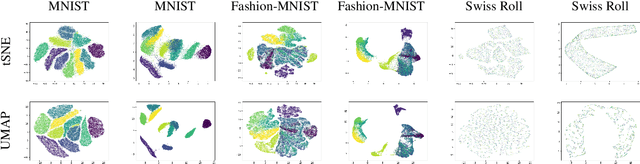
tSNE and UMAP are popular dimensionality reduction algorithms due to their speed and interpretable low-dimensional embeddings. Despite their popularity, however, little work has been done to study their full span of differences. We theoretically and experimentally evaluate the space of parameters in both tSNE and UMAP and observe that a single one -- the normalization -- is responsible for switching between them. This, in turn, implies that a majority of the algorithmic differences can be toggled without affecting the embeddings. We discuss the implications this has on several theoretic claims behind UMAP, as well as how to reconcile them with existing tSNE interpretations. Based on our analysis, we provide a method (\ourmethod) that combines previously incompatible techniques from tSNE and UMAP and can replicate the results of either algorithm. This allows our method to incorporate further improvements, such as an acceleration that obtains either method's outputs faster than UMAP. We release improved versions of tSNE, UMAP, and \ourmethod that are fully plug-and-play with the traditional libraries at https://github.com/Andrew-Draganov/GiDR-DUN

GiDR-DUN; Gradient Dimensionality Reduction -- Differences and Unification

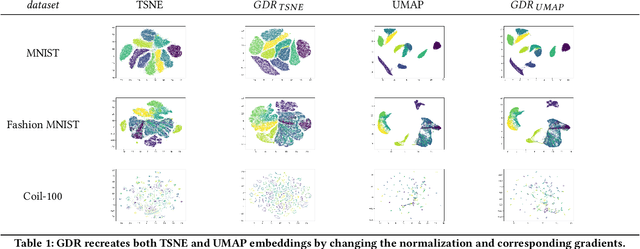
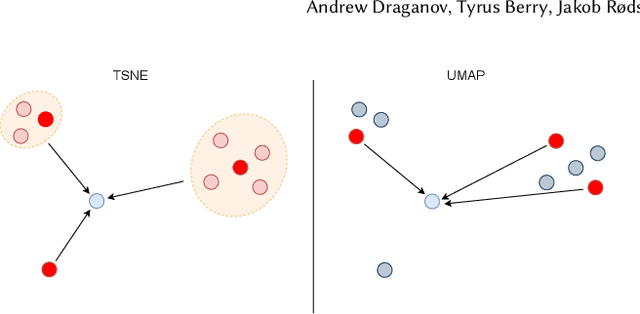
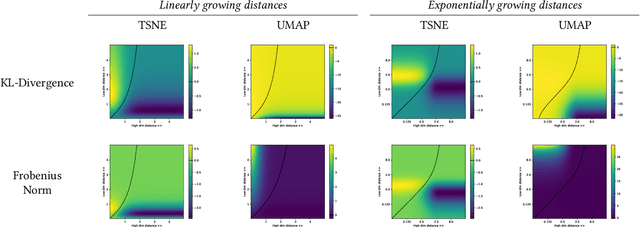
TSNE and UMAP are two of the most popular dimensionality reduction algorithms due to their speed and interpretable low-dimensional embeddings. However, while attempts have been made to improve on TSNE's computational complexity, no existing method can obtain TSNE embeddings at the speed of UMAP. In this work, we show that this is indeed possible by combining the two approaches into a single method. We theoretically and experimentally evaluate the full space of parameters in the TSNE and UMAP algorithms and observe that a single parameter, the normalization, is responsible for switching between them. This, in turn, implies that a majority of the algorithmic differences can be toggled without affecting the embeddings. We discuss the implications this has on several theoretic claims underpinning the UMAP framework, as well as how to reconcile them with existing TSNE interpretations. Based on our analysis, we propose a new dimensionality reduction algorithm, GDR, that combines previously incompatible techniques from TSNE and UMAP and can replicate the results of either algorithm by changing the normalization. As a further advantage, GDR performs the optimization faster than available UMAP methods and thus an order of magnitude faster than available TSNE methods. Our implementation is plug-and-play with the traditional UMAP and TSNE libraries and can be found at github.com/Andrew-Draganov/GiDR-DUN.