Practical Policy Optimization with Personalized Experimentation

Many organizations measure treatment effects via an experimentation platform to evaluate the casual effect of product variations prior to full-scale deployment. However, standard experimentation platforms do not perform optimally for end user populations that exhibit heterogeneous treatment effects (HTEs). Here we present a personalized experimentation framework, Personalized Experiments (PEX), which optimizes treatment group assignment at the user level via HTE modeling and sequential decision policy optimization to optimize multiple short-term and long-term outcomes simultaneously. We describe an end-to-end workflow that has proven to be successful in practice and can be readily implemented using open-source software.

Multi-armed Bandits with Cost Subsidy

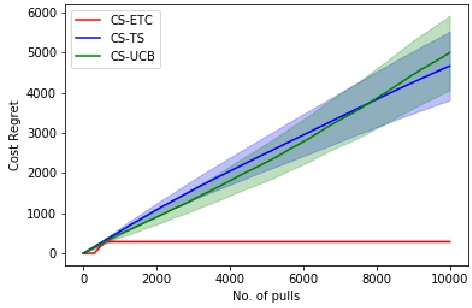
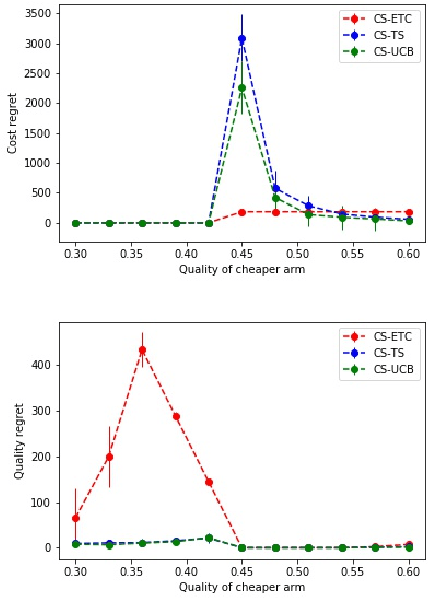
In this paper, we consider a novel variant of the multi-armed bandit (MAB) problem, MAB with cost subsidy, which models many real-life applications where the learning agent has to pay to select an arm and is concerned about optimizing cumulative costs and rewards. We present two applications, intelligent SMS routing problem and ad audience optimization problem faced by a number of businesses (especially online platforms) and show how our problem uniquely captures key features of these applications. We show that naive generalizations of existing MAB algorithms like Upper Confidence Bound and Thompson Sampling do not perform well for this problem. We then establish fundamental lower bound of $\Omega(K^{1/3} T^{2/3})$ on the performance of any online learning algorithm for this problem, highlighting the hardness of our problem in comparison to the classical MAB problem (where $T$ is the time horizon and $K$ is the number of arms). We also present a simple variant of explore-then-commit and establish near-optimal regret bounds for this algorithm. Lastly, we perform extensive numerical simulations to understand the behavior of a suite of algorithms for various instances and recommend a practical guide to employ different algorithms.

Active Learning for Skewed Data Sets

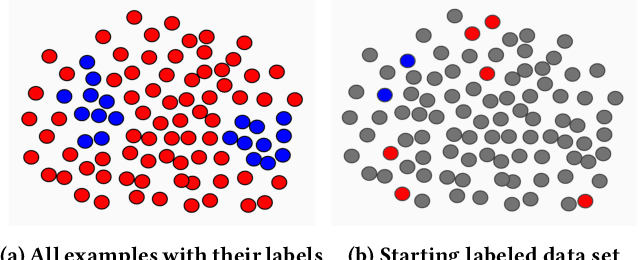
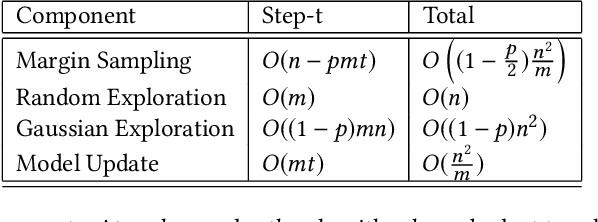
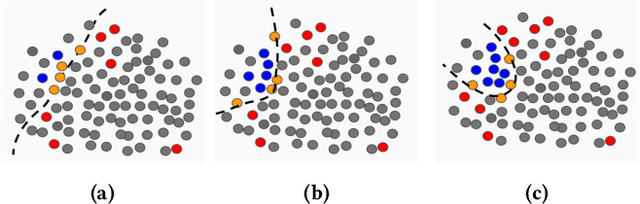
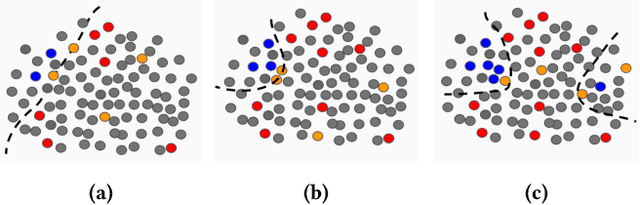
Consider a sequential active learning problem where, at each round, an agent selects a batch of unlabeled data points, queries their labels and updates a binary classifier. While there exists a rich body of work on active learning in this general form, in this paper, we focus on problems with two distinguishing characteristics: severe class imbalance (skew) and small amounts of initial training data. Both of these problems occur with surprising frequency in many web applications. For instance, detecting offensive or sensitive content in online communities (pornography, violence, and hate-speech) is receiving enormous attention from industry as well as research communities. Such problems have both the characteristics we describe -- a vast majority of content is not offensive, so the number of positive examples for such content is orders of magnitude smaller than the negative examples. Furthermore, there is usually only a small amount of initial training data available when building machine-learned models to solve such problems. To address both these issues, we propose a hybrid active learning algorithm (HAL) that balances exploiting the knowledge available through the currently labeled training examples with exploring the large amount of unlabeled data available. Through simulation results, we show that HAL makes significantly better choices for what points to label when compared to strong baselines like margin-sampling. Classifiers trained on the examples selected for labeling by HAL easily out-perform the baselines on target metrics (like area under the precision-recall curve) given the same budget for labeling examples. We believe HAL offers a simple, intuitive, and computationally tractable way to structure active learning for a wide range of machine learning applications.

Best Arm Identification in Generalized Linear Bandits

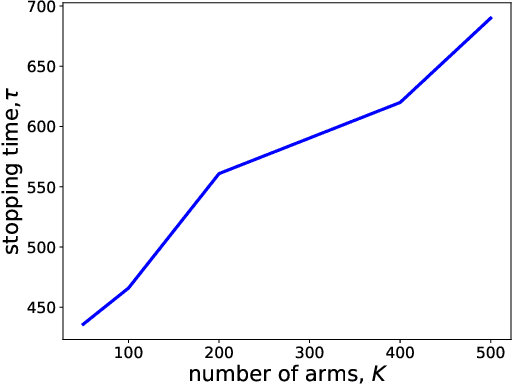
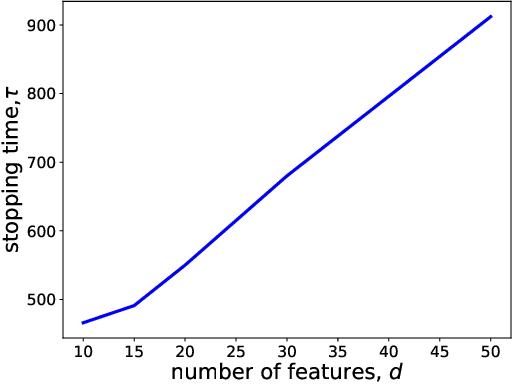
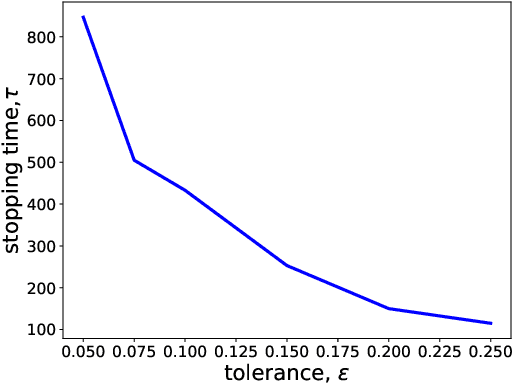
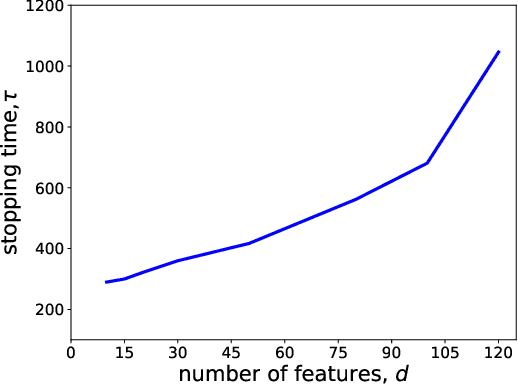
Motivated by drug design, we consider the best-arm identification problem in generalized linear bandits. More specifically, we assume each arm has a vector of covariates, there is an unknown vector of parameters that is common across the arms, and a generalized linear model captures the dependence of rewards on the covariate and parameter vectors. The problem is to minimize the number of arm pulls required to identify an arm that is sufficiently close to optimal with a sufficiently high probability. Building on recent progress in best-arm identification for linear bandits (Xu et al. 2018), we propose the first algorithm for best-arm identification for generalized linear bandits, provide theoretical guarantees on its accuracy and sampling efficiency, and evaluate its performance in various scenarios via simulation.

A Tutorial on Thompson Sampling

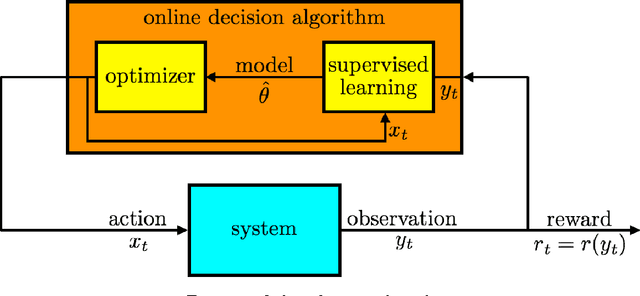
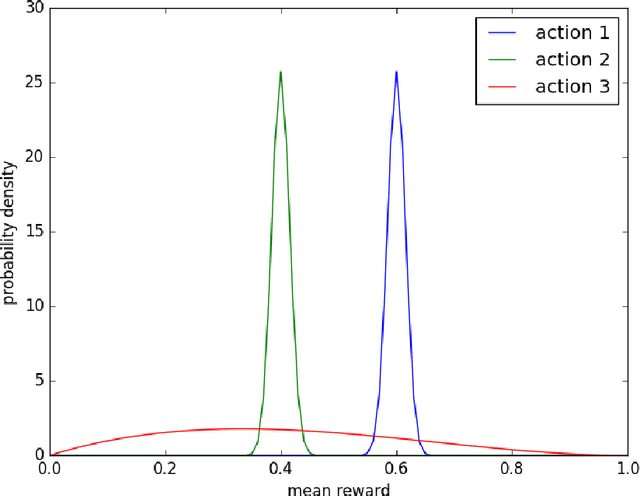
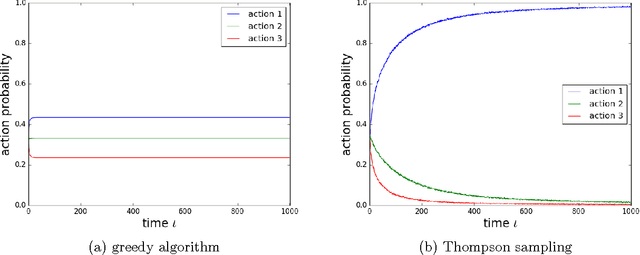
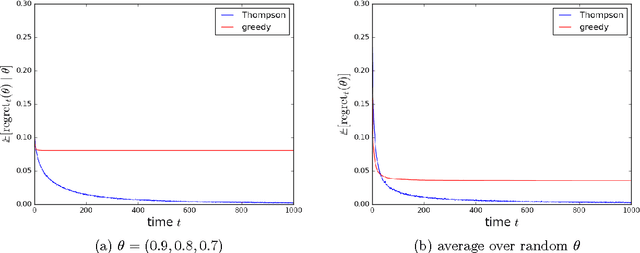
Thompson sampling is an algorithm for online decision problems where actions are taken sequentially in a manner that must balance between exploiting what is known to maximize immediate performance and investing to accumulate new information that may improve future performance. The algorithm addresses a broad range of problems in a computationally efficient manner and is therefore enjoying wide use. This tutorial covers the algorithm and its application, illustrating concepts through a range of examples, including Bernoulli bandit problems, shortest path problems, dynamic pricing, recommendation, active learning with neural networks, and reinforcement learning in Markov decision processes. Most of these problems involve complex information structures, where information revealed by taking an action informs beliefs about other actions. We will also discuss when and why Thompson sampling is or is not effective and relations to alternative algorithms.

Learning to Price with Reference Effects

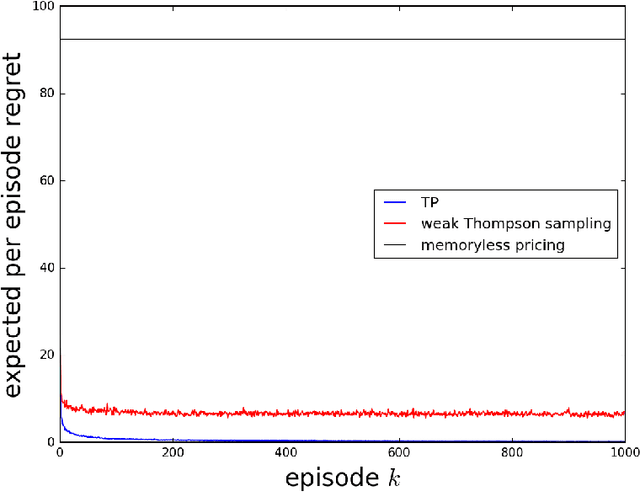
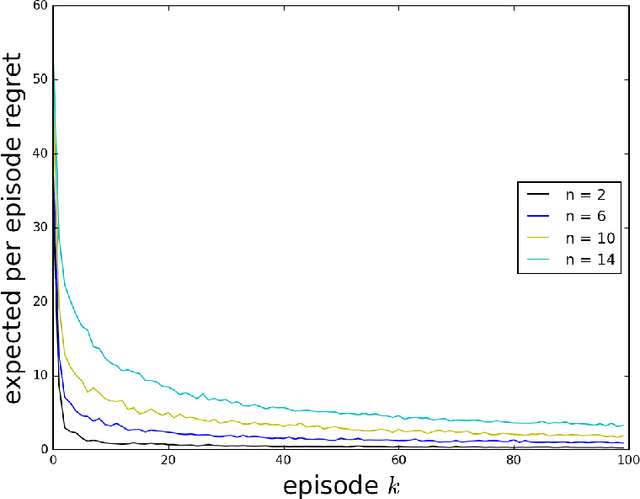
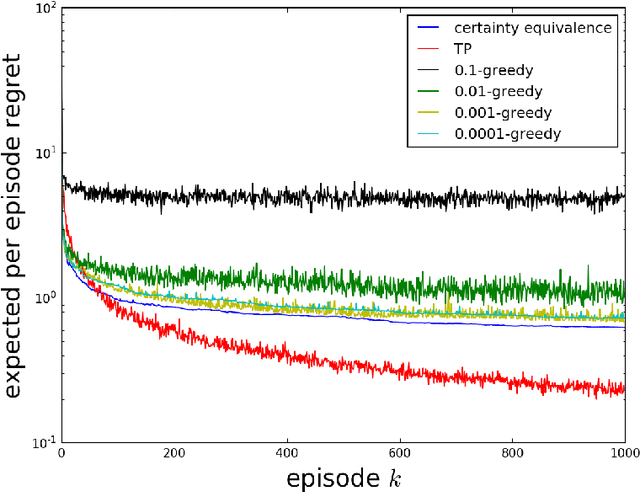
As a firm varies the price of a product, consumers exhibit reference effects, making purchase decisions based not only on the prevailing price but also the product's price history. We consider the problem of learning such behavioral patterns as a monopolist releases, markets, and prices products. This context calls for pricing decisions that intelligently trade off between maximizing revenue generated by a current product and probing to gain information for future benefit. Due to dependence on price history, realized demand can reflect delayed consequences of earlier pricing decisions. As such, inference entails attribution of outcomes to prior decisions and effective exploration requires planning price sequences that yield informative future outcomes. Despite the considerable complexity of this problem, we offer a tractable systematic approach. In particular, we frame the problem as one of reinforcement learning and leverage Thompson sampling. We also establish a regret bound that provides graceful guarantees on how performance improves as data is gathered and how this depends on the complexity of the demand model. We illustrate merits of the approach through simulations.

Conservative Contextual Linear Bandits

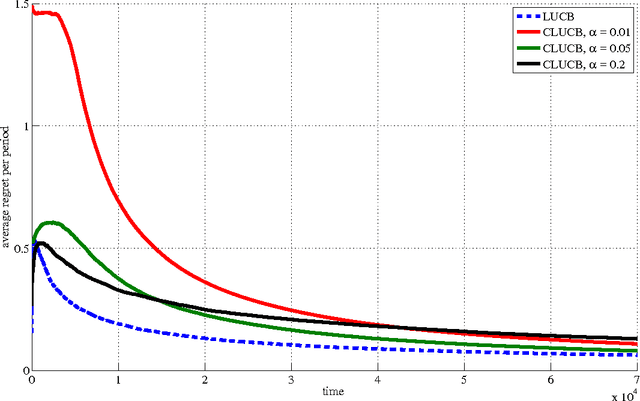
Safety is a desirable property that can immensely increase the applicability of learning algorithms in real-world decision-making problems. It is much easier for a company to deploy an algorithm that is safe, i.e., guaranteed to perform at least as well as a baseline. In this paper, we study the issue of safety in contextual linear bandits that have application in many different fields including personalized ad recommendation in online marketing. We formulate a notion of safety for this class of algorithms. We develop a safe contextual linear bandit algorithm, called conservative linear UCB (CLUCB), that simultaneously minimizes its regret and satisfies the safety constraint, i.e., maintains its performance above a fixed percentage of the performance of a baseline strategy, uniformly over time. We prove an upper-bound on the regret of CLUCB and show that it can be decomposed into two terms: 1) an upper-bound for the regret of the standard linear UCB algorithm that grows with the time horizon and 2) a constant (does not grow with the time horizon) term that accounts for the loss of being conservative in order to satisfy the safety constraint. We empirically show that our algorithm is safe and validate our theoretical analysis.