Lawrence M. Wein
Best Arm Identification in Generalized Linear Bandits
May 20, 2019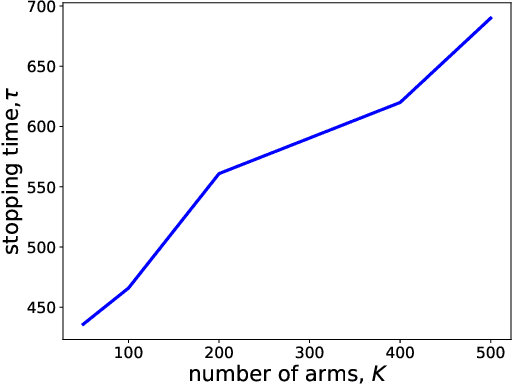
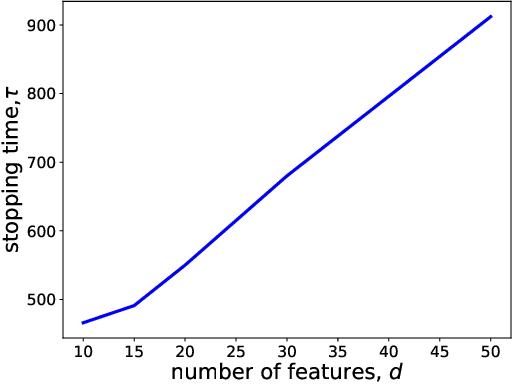
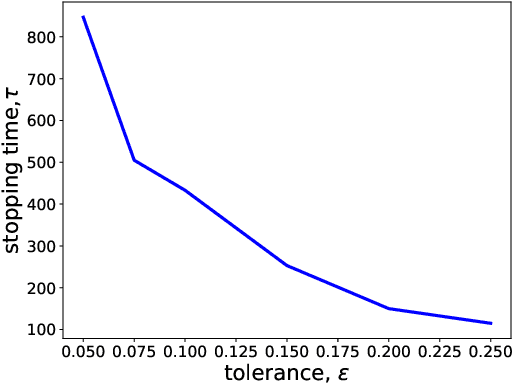
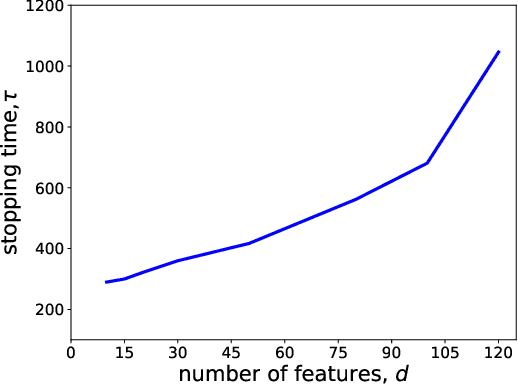
Abstract:Motivated by drug design, we consider the best-arm identification problem in generalized linear bandits. More specifically, we assume each arm has a vector of covariates, there is an unknown vector of parameters that is common across the arms, and a generalized linear model captures the dependence of rewards on the covariate and parameter vectors. The problem is to minimize the number of arm pulls required to identify an arm that is sufficiently close to optimal with a sufficiently high probability. Building on recent progress in best-arm identification for linear bandits (Xu et al. 2018), we propose the first algorithm for best-arm identification for generalized linear bandits, provide theoretical guarantees on its accuracy and sampling efficiency, and evaluate its performance in various scenarios via simulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge