Scale Free Adversarial Multi Armed Bandits

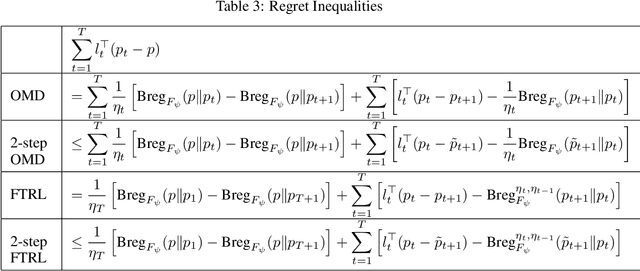
We consider the Scale-Free Adversarial Multi Armed Bandit(MAB) problem, where the player only knows the number of arms $n$ and not the scale or magnitude of the losses. It sees bandit feedback about the loss vectors $l_1,\dots, l_T \in \mathbb{R}^n$. The goal is to bound its regret as a function of $n$ and $l_1,\dots, l_T$. We design a Follow The Regularized Leader(FTRL) algorithm, which comes with the first scale-free regret guarantee for MAB. It uses the log barrier regularizer, the importance weighted estimator, an adaptive learning rate, and an adaptive exploration parameter. In the analysis, we introduce a simple, unifying technique for obtaining regret inequalities for FTRL and Online Mirror Descent(OMD) on the probability simplex using Potential Functions and Mixed Bregmans. We also develop a new technique for obtaining local-norm lower bounds for Bregman Divergences, which are crucial in bandit regret bounds. These tools could be of independent interest.

Exponential Weights on the Hypercube in Polynomial Time

We study a general online linear optimization problem(OLO). At each round, a subset of objects from a fixed universe of $n$ objects is chosen, and a linear cost associated with the chosen subset is incurred. We use regret as a measure of performance of our algorithms. Regret is the difference between the total cost incurred over all iterations and the cost of the best fixed subset in hindsight. We consider Full Information, Semi-Bandit and Bandit feedback for this problem. Using characteristic vectors of the subsets, this problem reduces to OLO on the $\{0,1\}^n$ hypercube. The Exp2 algorithm and its bandit variants are commonly used strategies for this problem. It was previously unknown if it is possible to run Exp2 on the hypercube in polynomial time. In this paper, we present a polynomial time algorithm called PolyExp for OLO on the hypercube. We show that our algorithm is equivalent to both Exp2 on $\{0,1\}^n$ as well as Online Mirror Descent(OMD) with Entropic regularization on $[0,1]^n$ and Bernoulli Sampling. We consider $L_\infty$ adversarial losses. We show PolyExp achieves expected regret bounds that are a factor of $\sqrt{n}$ better than Exp2 in all the three settings. Because of the equivalence of these algorithms, this implies an improvement on Exp2's regret bounds. Moreover, PolyExp's regret bounds match the $L_\infty$ lowerbounds in Audibert et al. (2011). Finally, we show how to use PolyExp on the $\{-1,+1\}^n$ hypercube, solving an open problem in Bubeck et al. (2012).

Efficient Reinforcement Learning via Initial Pure Exploration

In several realistic situations, an interactive learning agent can practice and refine its strategy before going on to be evaluated. For instance, consider a student preparing for a series of tests. She would typically take a few practice tests to know which areas she needs to improve upon. Based of the scores she obtains in these practice tests, she would formulate a strategy for maximizing her scores in the actual tests. We treat this scenario in the context of an agent exploring a fixed-horizon episodic Markov Decision Process (MDP), where the agent can practice on the MDP for some number of episodes (not necessarily known in advance) before starting to incur regret for its actions. During practice, the agent's goal must be to maximize the probability of following an optimal policy. This is akin to the problem of Pure Exploration (PE). We extend the PE problem of Multi Armed Bandits (MAB) to MDPs and propose a Bayesian algorithm called Posterior Sampling for Pure Exploration (PSPE), which is similar to its bandit counterpart. We show that the Bayesian simple regret converges at an optimal exponential rate when using PSPE. When the agent starts being evaluated, its goal would be to minimize the cumulative regret incurred. This is akin to the problem of Reinforcement Learning (RL). The agent uses the Posterior Sampling for Reinforcement Learning algorithm (PSRL) initialized with the posteriors of the practice phase. We hypothesize that this PSPE + PSRL combination is an optimal strategy for minimizing regret in RL problems with an initial practice phase. We show empirical results which prove that having a lower simple regret at the end of the practice phase results in having lower cumulative regret during evaluation.