Scale Free Adversarial Multi Armed Bandits

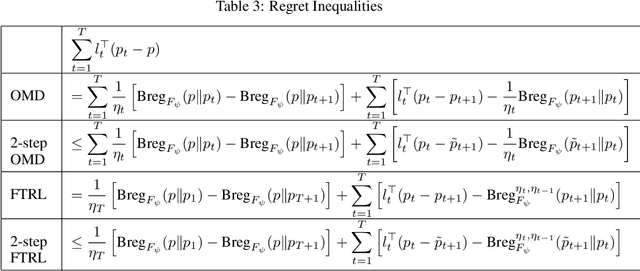
We consider the Scale-Free Adversarial Multi Armed Bandit(MAB) problem, where the player only knows the number of arms $n$ and not the scale or magnitude of the losses. It sees bandit feedback about the loss vectors $l_1,\dots, l_T \in \mathbb{R}^n$. The goal is to bound its regret as a function of $n$ and $l_1,\dots, l_T$. We design a Follow The Regularized Leader(FTRL) algorithm, which comes with the first scale-free regret guarantee for MAB. It uses the log barrier regularizer, the importance weighted estimator, an adaptive learning rate, and an adaptive exploration parameter. In the analysis, we introduce a simple, unifying technique for obtaining regret inequalities for FTRL and Online Mirror Descent(OMD) on the probability simplex using Potential Functions and Mixed Bregmans. We also develop a new technique for obtaining local-norm lower bounds for Bregman Divergences, which are crucial in bandit regret bounds. These tools could be of independent interest.