Optimistic Q-learning for average reward and episodic reinforcement learning
Paper and Code
Jul 18, 2024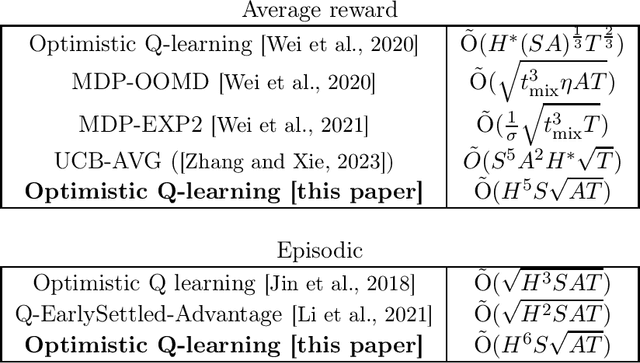
We present an optimistic Q-learning algorithm for regret minimization in average reward reinforcement learning under an additional assumption on the underlying MDP that for all policies, the expected time to visit some frequent state $s_0$ is finite and upper bounded by $H$. Our setting strictly generalizes the episodic setting and is significantly less restrictive than the assumption of bounded hitting time {\it for all states} made by most previous literature on model-free algorithms in average reward settings. We demonstrate a regret bound of $\tilde{O}(H^5 S\sqrt{AT})$, where $S$ and $A$ are the numbers of states and actions, and $T$ is the horizon. A key technical novelty of our work is to introduce an $\overline{L}$ operator defined as $\overline{L} v = \frac{1}{H} \sum_{h=1}^H L^h v$ where $L$ denotes the Bellman operator. We show that under the given assumption, the $\overline{L}$ operator has a strict contraction (in span) even in the average reward setting. Our algorithm design then uses ideas from episodic Q-learning to estimate and apply this operator iteratively. Therefore, we provide a unified view of regret minimization in episodic and non-episodic settings that may be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge