Kfir Yehuda Levy
Policy Gradient with Tree Search: Avoiding Local Optimas through Lookahead
Jun 08, 2025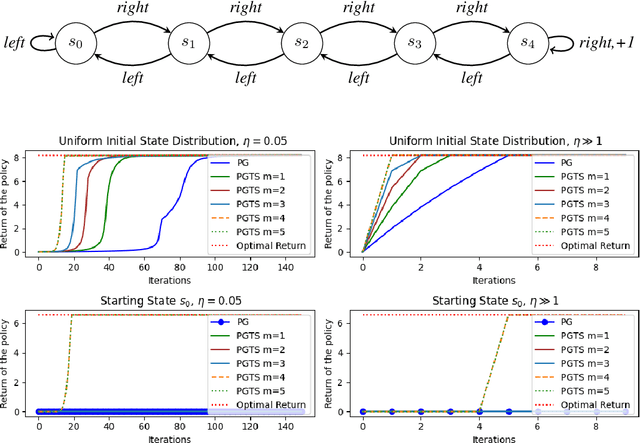
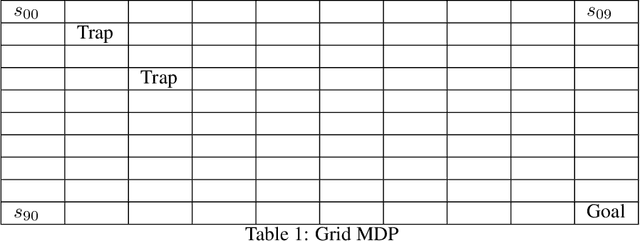
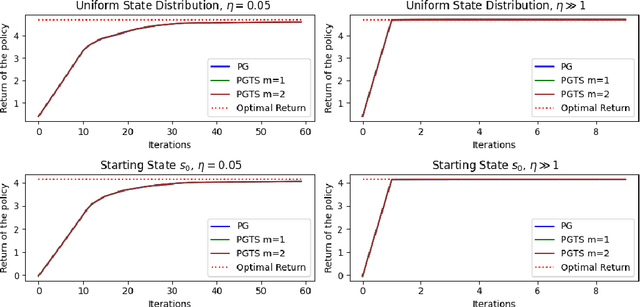

Abstract:Classical policy gradient (PG) methods in reinforcement learning frequently converge to suboptimal local optima, a challenge exacerbated in large or complex environments. This work investigates Policy Gradient with Tree Search (PGTS), an approach that integrates an $m$-step lookahead mechanism to enhance policy optimization. We provide theoretical analysis demonstrating that increasing the tree search depth $m$-monotonically reduces the set of undesirable stationary points and, consequently, improves the worst-case performance of any resulting stationary policy. Critically, our analysis accommodates practical scenarios where policy updates are restricted to states visited by the current policy, rather than requiring updates across the entire state space. Empirical evaluations on diverse MDP structures, including Ladder, Tightrope, and Gridworld environments, illustrate PGTS's ability to exhibit "farsightedness," navigate challenging reward landscapes, escape local traps where standard PG fails, and achieve superior solutions.
Dual Formulation for Non-Rectangular Lp Robust Markov Decision Processes
Feb 13, 2025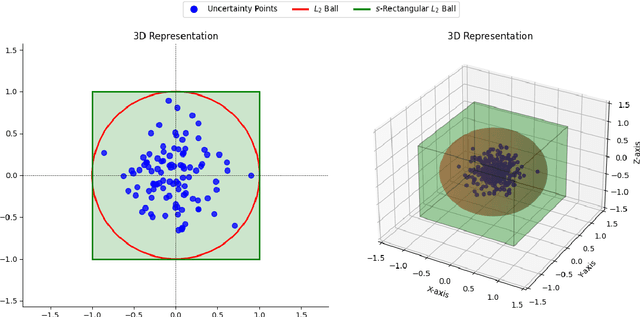

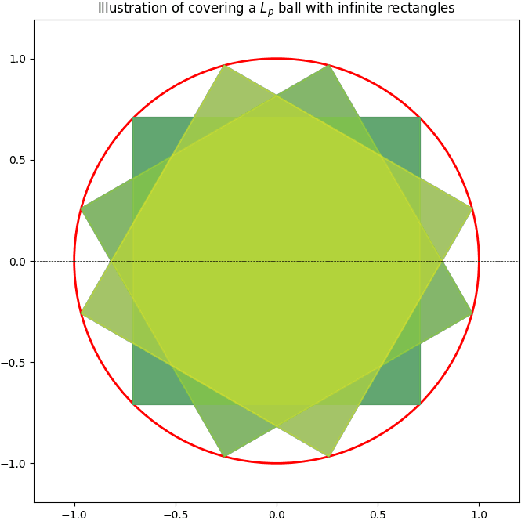

Abstract:We study robust Markov decision processes (RMDPs) with non-rectangular uncertainty sets, which capture interdependencies across states unlike traditional rectangular models. While non-rectangular robust policy evaluation is generally NP-hard, even in approximation, we identify a powerful class of $L_p$-bounded uncertainty sets that avoid these complexity barriers due to their structural simplicity. We further show that this class can be decomposed into infinitely many \texttt{sa}-rectangular $L_p$-bounded sets and leverage its structural properties to derive a novel dual formulation for $L_p$ RMDPs. This formulation provides key insights into the adversary's strategy and enables the development of the first robust policy evaluation algorithms for non-rectangular RMDPs. Empirical results demonstrate that our approach significantly outperforms brute-force methods, establishing a promising foundation for future investigation into non-rectangular robust MDPs.
Improved Sample Complexity for Global Convergence of Actor-Critic Algorithms
Oct 11, 2024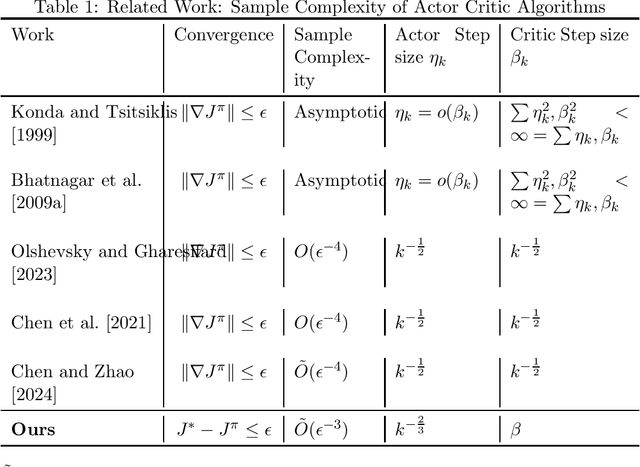
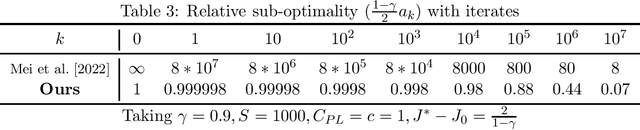
Abstract:In this paper, we establish the global convergence of the actor-critic algorithm with a significantly improved sample complexity of $O(\epsilon^{-3})$, advancing beyond the existing local convergence results. Previous works provide local convergence guarantees with a sample complexity of $O(\epsilon^{-2})$ for bounding the squared gradient of the return, which translates to a global sample complexity of $O(\epsilon^{-4})$ using the gradient domination lemma. In contrast to traditional methods that employ decreasing step sizes for both the actor and critic, we demonstrate that a constant step size for the critic is sufficient to ensure convergence in expectation. This key insight reveals that using a decreasing step size for the actor alone is sufficient to handle the noise for both the actor and critic. Our findings provide theoretical support for the practical success of many algorithms that rely on constant step sizes.
EXAQ: Exponent Aware Quantization For LLMs Acceleration
Oct 04, 2024



Abstract:Quantization has established itself as the primary approach for decreasing the computational and storage expenses associated with Large Language Models (LLMs) inference. The majority of current research emphasizes quantizing weights and activations to enable low-bit general-matrix-multiply (GEMM) operations, with the remaining non-linear operations executed at higher precision. In our study, we discovered that following the application of these techniques, the primary bottleneck in LLMs inference lies in the softmax layer. The softmax operation comprises three phases: exponent calculation, accumulation, and normalization, Our work focuses on optimizing the first two phases. We propose an analytical approach to determine the optimal clipping value for the input to the softmax function, enabling sub-4-bit quantization for LLMs inference. This method accelerates the calculations of both $e^x$ and $\sum(e^x)$ with minimal to no accuracy degradation. For example, in LLaMA1-30B, we achieve baseline performance with 2-bit quantization on the well-known "Physical Interaction: Question Answering" (PIQA) dataset evaluation. This ultra-low bit quantization allows, for the first time, an acceleration of approximately 4x in the accumulation phase. The combination of accelerating both $e^x$ and $\sum(e^x)$ results in a 36.9% acceleration in the softmax operation.
DropCompute: simple and more robust distributed synchronous training via compute variance reduction
Jun 18, 2023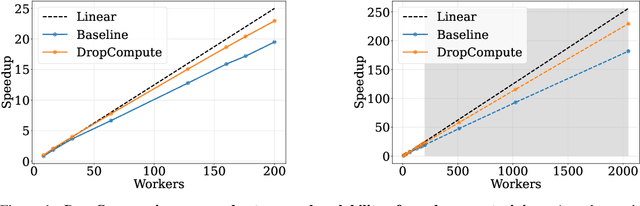

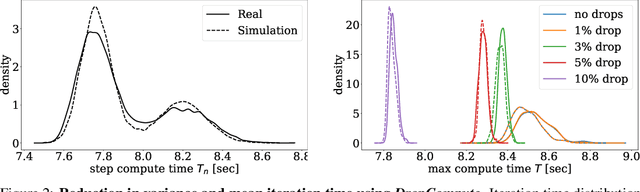
Abstract:Background: Distributed training is essential for large scale training of deep neural networks (DNNs). The dominant methods for large scale DNN training are synchronous (e.g. All-Reduce), but these require waiting for all workers in each step. Thus, these methods are limited by the delays caused by straggling workers. Results: We study a typical scenario in which workers are straggling due to variability in compute time. We find an analytical relation between compute time properties and scalability limitations, caused by such straggling workers. With these findings, we propose a simple yet effective decentralized method to reduce the variation among workers and thus improve the robustness of synchronous training. This method can be integrated with the widely used All-Reduce. Our findings are validated on large-scale training tasks using 200 Gaudi Accelerators.
High Probability Bounds for a Class of Nonconvex Algorithms with AdaGrad Stepsize
Apr 06, 2022
Abstract:In this paper, we propose a new, simplified high probability analysis of AdaGrad for smooth, non-convex problems. More specifically, we focus on a particular accelerated gradient (AGD) template (Lan, 2020), through which we recover the original AdaGrad and its variant with averaging, and prove a convergence rate of $\mathcal O (1/ \sqrt{T})$ with high probability without the knowledge of smoothness and variance. We use a particular version of Freedman's concentration bound for martingale difference sequences (Kakade & Tewari, 2008) which enables us to achieve the best-known dependence of $\log (1 / \delta )$ on the probability margin $\delta$. We present our analysis in a modular way and obtain a complementary $\mathcal O (1 / T)$ convergence rate in the deterministic setting. To the best of our knowledge, this is the first high probability result for AdaGrad with a truly adaptive scheme, i.e., completely oblivious to the knowledge of smoothness and uniform variance bound, which simultaneously has best-known dependence of $\log( 1/ \delta)$. We further prove noise adaptation property of AdaGrad under additional noise assumptions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge