EXAQ: Exponent Aware Quantization For LLMs Acceleration

Quantization has established itself as the primary approach for decreasing the computational and storage expenses associated with Large Language Models (LLMs) inference. The majority of current research emphasizes quantizing weights and activations to enable low-bit general-matrix-multiply (GEMM) operations, with the remaining non-linear operations executed at higher precision. In our study, we discovered that following the application of these techniques, the primary bottleneck in LLMs inference lies in the softmax layer. The softmax operation comprises three phases: exponent calculation, accumulation, and normalization, Our work focuses on optimizing the first two phases. We propose an analytical approach to determine the optimal clipping value for the input to the softmax function, enabling sub-4-bit quantization for LLMs inference. This method accelerates the calculations of both $e^x$ and $\sum(e^x)$ with minimal to no accuracy degradation. For example, in LLaMA1-30B, we achieve baseline performance with 2-bit quantization on the well-known "Physical Interaction: Question Answering" (PIQA) dataset evaluation. This ultra-low bit quantization allows, for the first time, an acceleration of approximately 4x in the accumulation phase. The combination of accelerating both $e^x$ and $\sum(e^x)$ results in a 36.9% acceleration in the softmax operation.

Bimodal Distributed Binarized Neural Networks

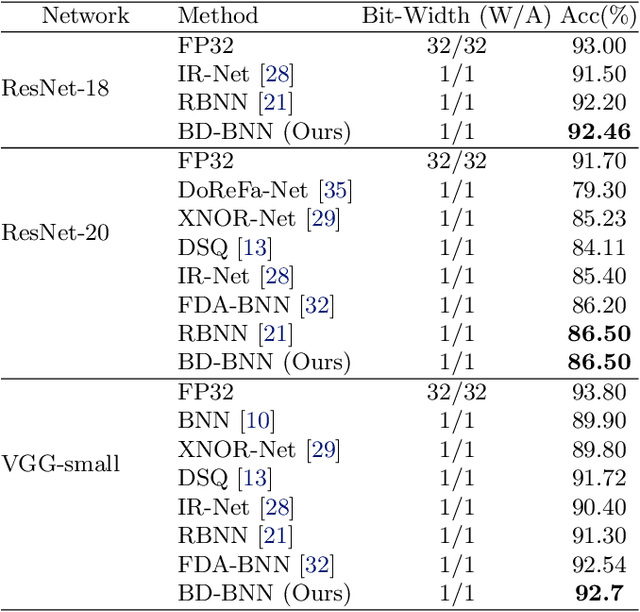
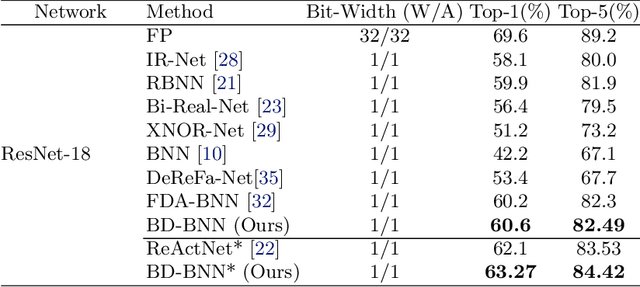
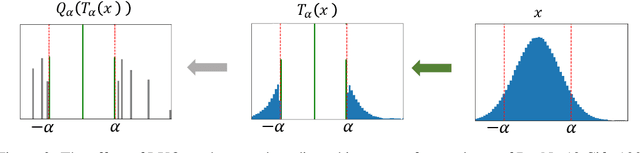
Binary Neural Networks (BNNs) are an extremely promising method to reduce deep neural networks' complexity and power consumption massively. Binarization techniques, however, suffer from ineligible performance degradation compared to their full-precision counterparts. Prior work mainly focused on strategies for sign function approximation during forward and backward phases to reduce the quantization error during the binarization process. In this work, we propose a Bi-Modal Distributed binarization method (\methodname{}). That imposes bi-modal distribution of the network weights by kurtosis regularization. The proposed method consists of a training scheme that we call Weight Distribution Mimicking (WDM), which efficiently imitates the full-precision network weight distribution to their binary counterpart. Preserving this distribution during binarization-aware training creates robust and informative binary feature maps and significantly reduces the generalization error of the BNN. Extensive evaluations on CIFAR-10 and ImageNet demonstrate the superiority of our method over current state-of-the-art schemes. Our source code, experimental settings, training logs, and binary models are available at \url{https://github.com/BlueAnon/BD-BNN}.

Optimal Fine-Grained N:M sparsity for Activations and Neural Gradients

In deep learning, fine-grained N:M sparsity reduces the data footprint and bandwidth of a General Matrix multiply (GEMM) by x2, and doubles throughput by skipping computation of zero values. So far, it was only used to prune weights. We examine how this method can be used also for activations and their gradients (i.e., "neural gradients"). To this end, we first establish tensor-level optimality criteria. Previous works aimed to minimize the mean-square-error (MSE) of each pruned block. We show that while minimization of the MSE works fine for pruning the activations, it catastrophically fails for the neural gradients. Instead, we show that optimal pruning of the neural gradients requires an unbiased minimum-variance pruning mask. We design such specialized masks, and find that in most cases, 1:2 sparsity is sufficient for training, and 2:4 sparsity is usually enough when this is not the case. Further, we suggest combining several such methods together in order to speed up training even more. A reference implementation is supplied in https://github.com/brianchmiel/Act-and-Grad-structured-sparsity.

Logarithmic Unbiased Quantization: Practical 4-bit Training in Deep Learning

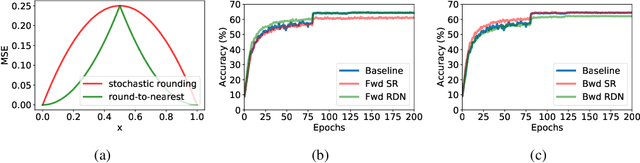
Quantization of the weights and activations is one of the main methods to reduce the computational footprint of Deep Neural Networks (DNNs) training. Current methods enable 4-bit quantization of the forward phase. However, this constitutes only a third of the training process. Reducing the computational footprint of the entire training process requires the quantization of the neural gradients, i.e., the loss gradients with respect to the outputs of intermediate neural layers. In this work, we examine the importance of having unbiased quantization in quantized neural network training, where to maintain it, and how. Based on this, we suggest a $\textit{logarithmic unbiased quantization}$ (LUQ) method to quantize both the forward and backward phase to 4-bit, achieving state-of-the-art results in 4-bit training without overhead. For example, in ResNet50 on ImageNet, we achieved a degradation of 1.18%. We further improve this to degradation of only 0.64% after a single epoch of high precision fine-tuning combined with a variance reduction method -- both add overhead comparable to previously suggested methods. Finally, we suggest a method that uses the low precision format to avoid multiplications during two-thirds of the training process, thus reducing by 5x the area used by the multiplier.

Accelerated Sparse Neural Training: A Provable and Efficient Method to Find N:M Transposable Masks

Recently, researchers proposed pruning deep neural network weights (DNNs) using an $N:M$ fine-grained block sparsity mask. In this mask, for each block of $M$ weights, we have at least $N$ zeros. In contrast to unstructured sparsity, $N:M$ fine-grained block sparsity allows acceleration in actual modern hardware. So far, this was used for DNN acceleration at the inference phase. First, we suggest a method to convert a pretrained model with unstructured sparsity to a $N:M$ fine-grained block sparsity model, with little to no training. Then, to also allow such acceleration in the training phase, we suggest a novel transposable-fine-grained sparsity mask where the same mask can be used for both forward and backward passes. Our transposable mask ensures that both the weight matrix and its transpose follow the same sparsity pattern; thus the matrix multiplication required for passing the error backward can also be accelerated. We discuss the transposable constraint and devise a new measure for mask constraints, called mask-diversity (MD), which correlates with their expected accuracy. Then, we formulate the problem of finding the optimal transposable mask as a minimum-cost-flow problem and suggest a fast linear approximation that can be used when the masks dynamically change while training. Our experiments suggest 2x speed-up with no accuracy degradation over vision and language models. A reference implementation can be found at https://github.com/papers-submission/structured_transposable_masks.

Neural gradients are lognormally distributed: understanding sparse and quantized training

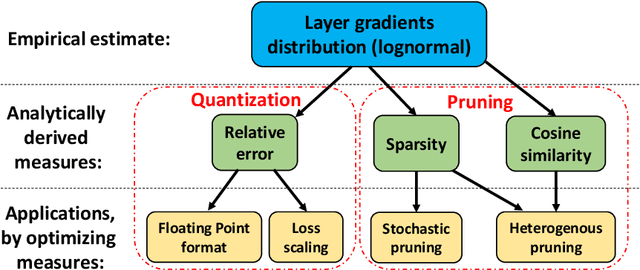
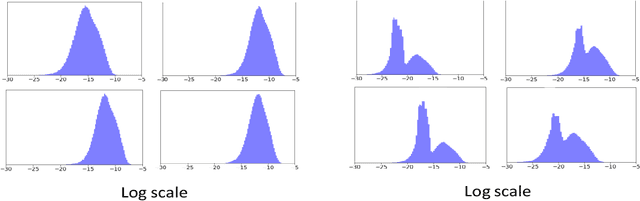
Neural gradient compression remains a main bottleneck in improving training efficiency, as most existing neural network compression methods (e.g., pruning or quantization) focus on weights, activations, and weight gradients. However, these methods are not suitable for compressing neural gradients, which have a very different distribution. Specifically, we find that the neural gradients follow a lognormal distribution. Taking this into account, we suggest two methods to reduce the computational and memory burdens of neural gradients. The first one is stochastic gradient pruning, which can accurately set the sparsity level -- up to 85% gradient sparsity without hurting validation accuracy (ResNet18 on ImageNet). The second method determines the floating-point format for low numerical precision gradients (e.g., FP8). Our results shed light on previous findings related to local scaling, the optimal bit-allocation for the mantissa and exponent, and challenging workloads for which low-precision floating-point arithmetic has reported to fail. Reference implementation accompanies the paper.

Colored Noise Injection for Training Adversarially Robust Neural Networks

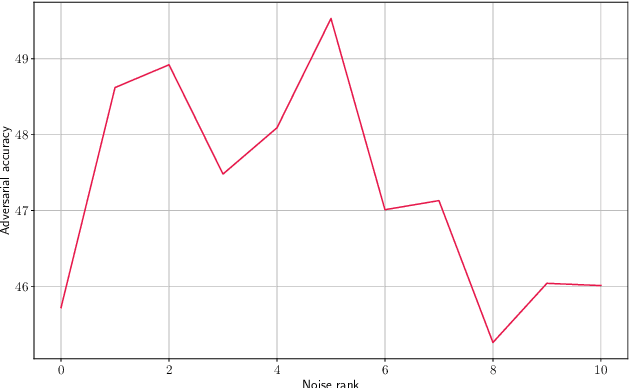
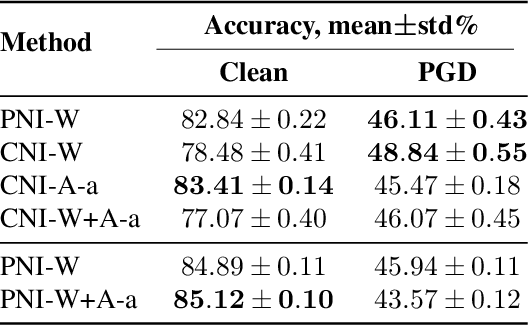
Even though deep learning has shown unmatched performance on various tasks, neural networks have been shown to be vulnerable to small adversarial perturbations of the input that lead to significant performance degradation. In this work we extend the idea of adding white Gaussian noise to the network weights and activations during adversarial training (PNI) to the injection of colored noise for defense against common white-box and black-box attacks. We show that our approach outperforms PNI and various previous approaches in terms of adversarial accuracy on CIFAR-10 and CIFAR-100 datasets. In addition, we provide an extensive ablation study of the proposed method justifying the chosen configurations.

Robust Quantization: One Model to Rule Them All

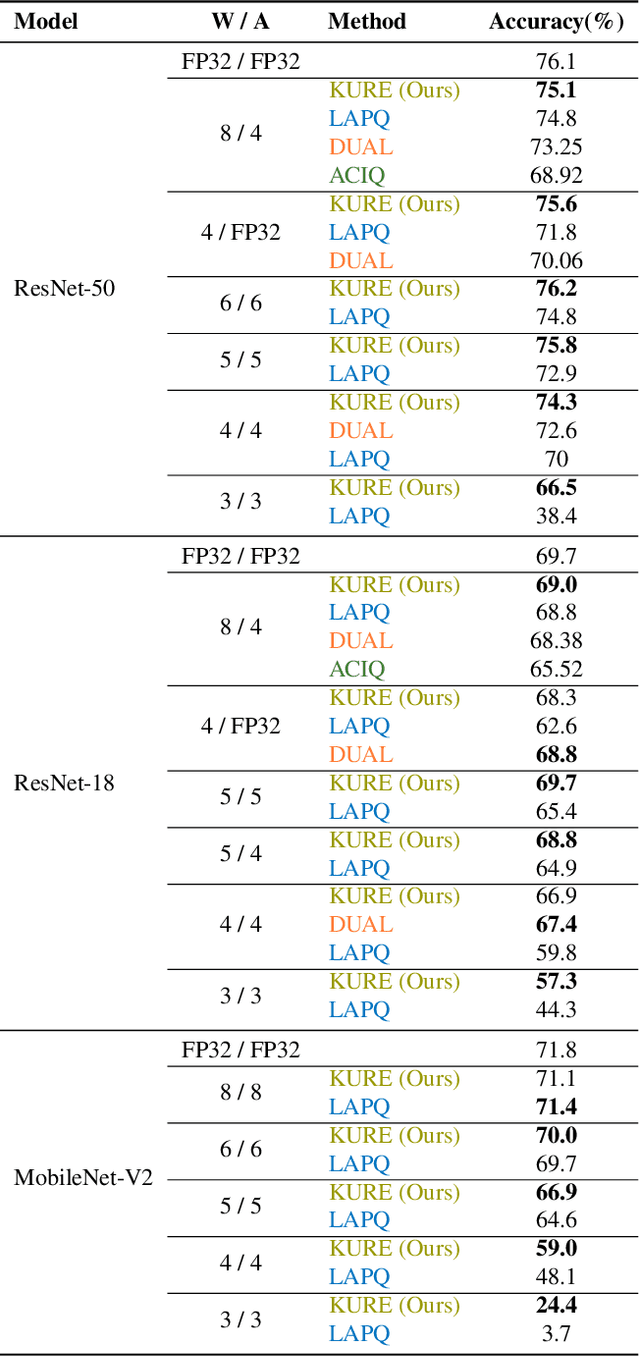
Neural network quantization methods often involve simulating the quantization process during training. This makes the trained model highly dependent on the precise way quantization is performed. Since low-precision accelerators differ in their quantization policies and their supported mix of data-types, a model trained for one accelerator may not be suitable for another. To address this issue, we propose KURE, a method that provides intrinsic robustness to the model against a broad range of quantization implementations. We show that KURE yields a generic model that may be deployed on numerous inference accelerators without a significant loss in accuracy.

Smoothed Inference for Adversarially-Trained Models

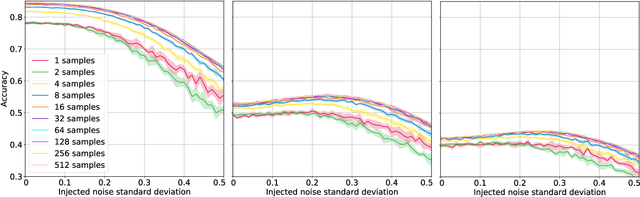
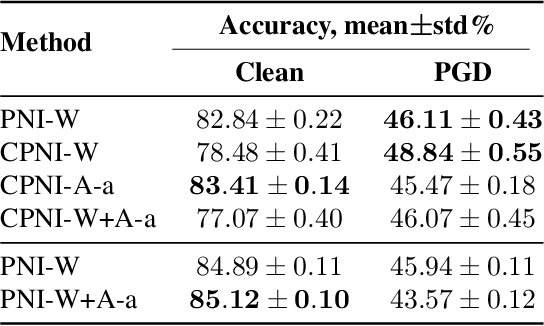
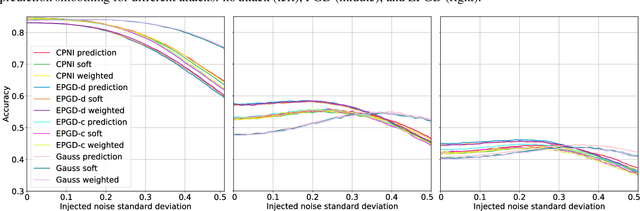
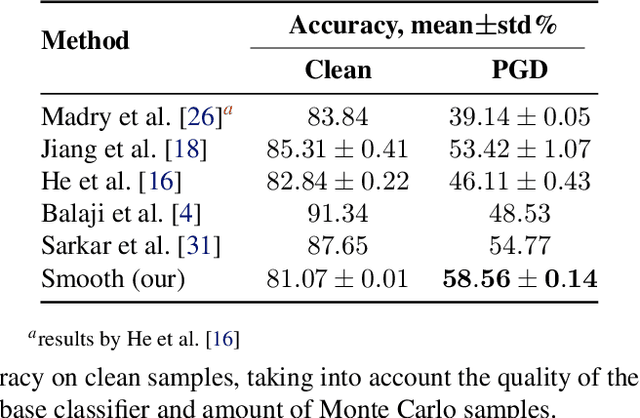
Deep neural networks are known to be vulnerable to inputs with maliciously constructed adversarial perturbations aimed at forcing misclassification. We study randomized smoothing as a way to both improve performance on unperturbed data as well as increase robustness to adversarial attacks. Moreover, we extend the method proposed by arXiv:1811.09310 by adding low-rank multivariate noise, which we then use as a base model for smoothing. The proposed method achieves 58.5% top-1 accuracy on CIFAR-10 under PGD attack and outperforms previous works by 4%. In addition, we consider a family of attacks, which were previously used for training purposes in the certified robustness scheme. We demonstrate that the proposed attacks are more effective than PGD against both smoothed and non-smoothed models. Since our method is based on sampling, it lends itself well for trading-off between the model inference complexity and its performance. A reference implementation of the proposed techniques is provided at https://github.com/yanemcovsky/SIAM.

Loss Aware Post-training Quantization

Neural network quantization enables the deployment of large models on resource-constrained devices. Current post-training quantization methods fall short in terms of accuracy for INT4 (or lower) but provide reasonable accuracy for INT8 (or above). In this work, we study the effect of quantization on the structure of the loss landscape. We show that the structure is flat and separable for mild quantization, enabling straightforward post-training quantization methods to achieve good results. On the other hand, we show that with more aggressive quantization, the loss landscape becomes highly non-separable with sharp minima points, making the selection of quantization parameters more challenging. Armed with this understanding, we design a method that quantizes the layer parameters jointly, enabling significant accuracy improvement over current post-training quantization methods. Reference implementation accompanies the paper at https://github.com/ynahshan/nn-quantization-pytorch/tree/master/lapq