Silenced Biases: The Dark Side LLMs Learned to Refuse

Safety-aligned large language models (LLMs) are becoming increasingly widespread, especially in sensitive applications where fairness is essential and biased outputs can cause significant harm. However, evaluating the fairness of models is a complex challenge, and approaches that do so typically utilize standard question-answer (QA) styled schemes. Such methods often overlook deeper issues by interpreting the model's refusal responses as positive fairness measurements, which creates a false sense of fairness. In this work, we introduce the concept of silenced biases, which are unfair preferences encoded within models' latent space and are effectively concealed by safety-alignment. Previous approaches that considered similar indirect biases often relied on prompt manipulation or handcrafted implicit queries, which present limited scalability and risk contaminating the evaluation process with additional biases. We propose the Silenced Bias Benchmark (SBB), which aims to uncover these biases by employing activation steering to reduce model refusals during QA. SBB supports easy expansion to new demographic groups and subjects, presenting a fairness evaluation framework that encourages the future development of fair models and tools beyond the masking effects of alignment training. We demonstrate our approach over multiple LLMs, where our findings expose an alarming distinction between models' direct responses and their underlying fairness issues.

Representing LLMs in Prompt Semantic Task Space

Large language models (LLMs) achieve impressive results over various tasks, and ever-expanding public repositories contain an abundance of pre-trained models. Therefore, identifying the best-performing LLM for a given task is a significant challenge. Previous works have suggested learning LLM representations to address this. However, these approaches present limited scalability and require costly retraining to encompass additional models and datasets. Moreover, the produced representation utilizes distinct spaces that cannot be easily interpreted. This work presents an efficient, training-free approach to representing LLMs as linear operators within the prompts' semantic task space, thus providing a highly interpretable representation of the models' application. Our method utilizes closed-form computation of geometrical properties and ensures exceptional scalability and real-time adaptability to dynamically expanding repositories. We demonstrate our approach on success prediction and model selection tasks, achieving competitive or state-of-the-art results with notable performance in out-of-sample scenarios.

Sparse patches adversarial attacks via extrapolating point-wise information

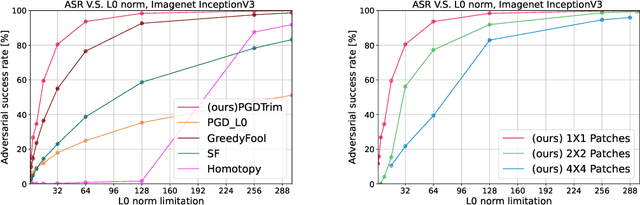
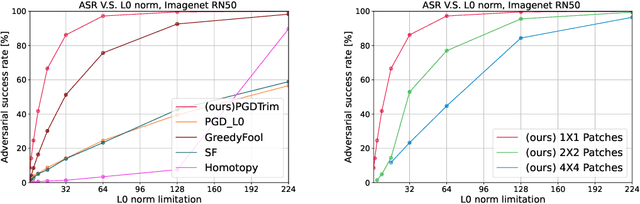
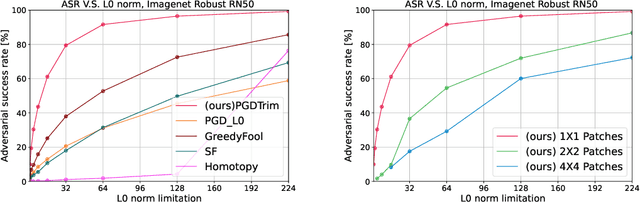
Sparse and patch adversarial attacks were previously shown to be applicable in realistic settings and are considered a security risk to autonomous systems. Sparse adversarial perturbations constitute a setting in which the adversarial perturbations are limited to affecting a relatively small number of points in the input. Patch adversarial attacks denote the setting where the sparse attacks are limited to a given structure, i.e., sparse patches with a given shape and number. However, previous patch adversarial attacks do not simultaneously optimize multiple patches' locations and perturbations. This work suggests a novel approach for sparse patches adversarial attacks via point-wise trimming dense adversarial perturbations. Our approach enables simultaneous optimization of multiple sparse patches' locations and perturbations for any given number and shape. Moreover, our approach is also applicable for standard sparse adversarial attacks, where we show that it significantly improves the state-of-the-art over multiple extensive settings. A reference implementation of the proposed method and the reported experiments is provided at \url{https://github.com/yanemcovsky/SparsePatches.git}

Physical Passive Patch Adversarial Attacks on Visual Odometry Systems

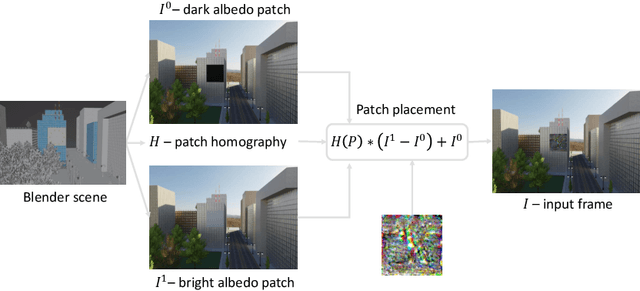
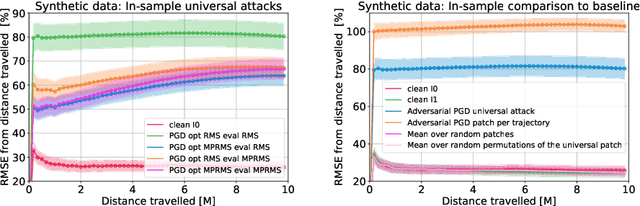
Deep neural networks are known to be susceptible to adversarial perturbations -- small perturbations that alter the output of the network and exist under strict norm limitations. While such perturbations are usually discussed as tailored to a specific input, a universal perturbation can be constructed to alter the model's output on a set of inputs. Universal perturbations present a more realistic case of adversarial attacks, as awareness of the model's exact input is not required. In addition, the universal attack setting raises the subject of generalization to unseen data, where given a set of inputs, the universal perturbations aim to alter the model's output on out-of-sample data. In this work, we study physical passive patch adversarial attacks on visual odometry-based autonomous navigation systems. A visual odometry system aims to infer the relative camera motion between two corresponding viewpoints, and is frequently used by vision-based autonomous navigation systems to estimate their state. For such navigation systems, a patch adversarial perturbation poses a severe security issue, as it can be used to mislead a system onto some collision course. To the best of our knowledge, we show for the first time that the error margin of a visual odometry model can be significantly increased by deploying patch adversarial attacks in the scene. We provide evaluation on synthetic closed-loop drone navigation data and demonstrate that a comparable vulnerability exists in real data. A reference implementation of the proposed method and the reported experiments is provided at https://github.com/patchadversarialattacks/patchadversarialattacks.

Colored Noise Injection for Training Adversarially Robust Neural Networks

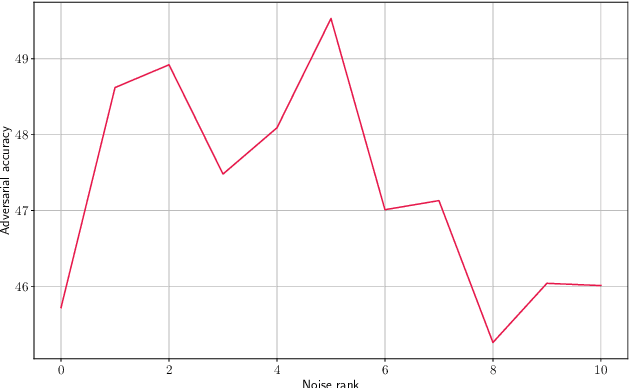
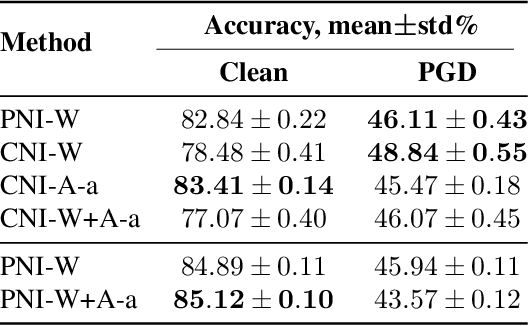
Even though deep learning has shown unmatched performance on various tasks, neural networks have been shown to be vulnerable to small adversarial perturbations of the input that lead to significant performance degradation. In this work we extend the idea of adding white Gaussian noise to the network weights and activations during adversarial training (PNI) to the injection of colored noise for defense against common white-box and black-box attacks. We show that our approach outperforms PNI and various previous approaches in terms of adversarial accuracy on CIFAR-10 and CIFAR-100 datasets. In addition, we provide an extensive ablation study of the proposed method justifying the chosen configurations.

On the generalization of bayesian deep nets for multi-class classification

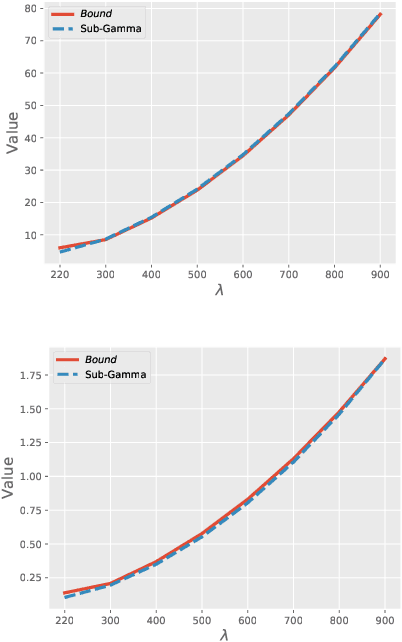
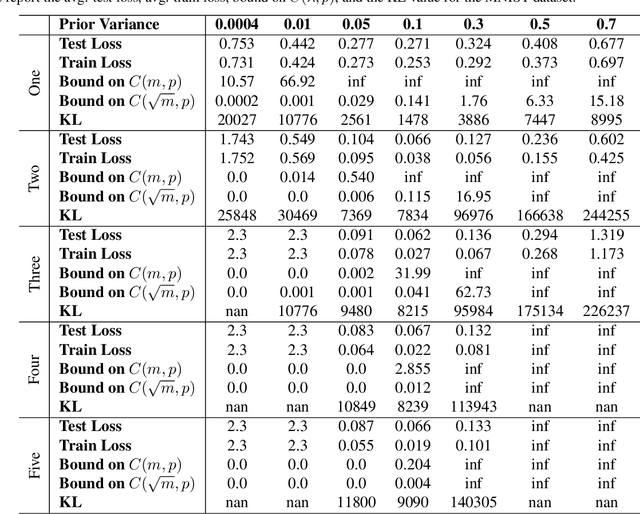
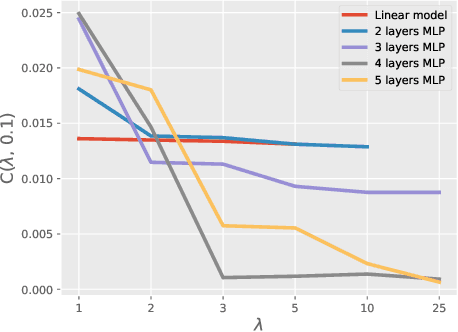
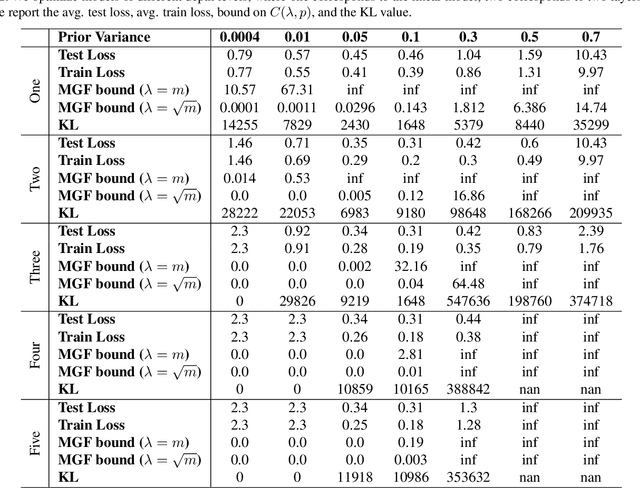
Generalization bounds which assess the difference between the true risk and the empirical risk have been studied extensively. However, to obtain bounds, current techniques use strict assumptions such as a uniformly bounded or a Lipschitz loss function. To avoid these assumptions, in this paper, we propose a new generalization bound for Bayesian deep nets by exploiting the contractivity of the Log-Sobolev inequalities. Using these inequalities adds an additional loss-gradient norm term to the generalization bound, which is intuitively a surrogate of the model complexity. Empirically, we analyze the affect of this loss-gradient norm term using different deep nets.

Smoothed Inference for Adversarially-Trained Models

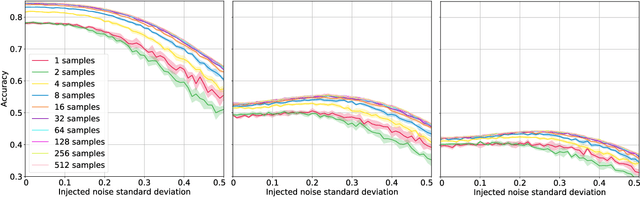
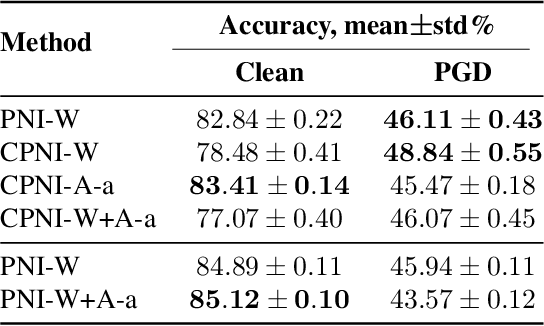
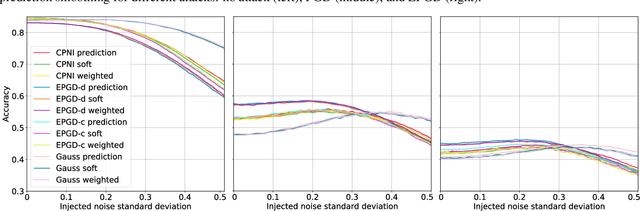
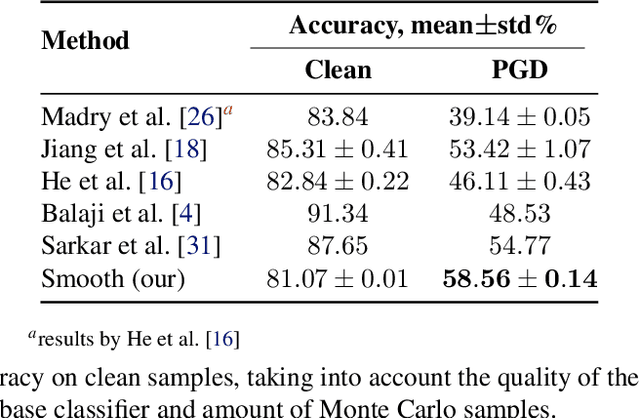
Deep neural networks are known to be vulnerable to inputs with maliciously constructed adversarial perturbations aimed at forcing misclassification. We study randomized smoothing as a way to both improve performance on unperturbed data as well as increase robustness to adversarial attacks. Moreover, we extend the method proposed by arXiv:1811.09310 by adding low-rank multivariate noise, which we then use as a base model for smoothing. The proposed method achieves 58.5% top-1 accuracy on CIFAR-10 under PGD attack and outperforms previous works by 4%. In addition, we consider a family of attacks, which were previously used for training purposes in the certified robustness scheme. We demonstrate that the proposed attacks are more effective than PGD against both smoothed and non-smoothed models. Since our method is based on sampling, it lends itself well for trading-off between the model inference complexity and its performance. A reference implementation of the proposed techniques is provided at https://github.com/yanemcovsky/SIAM.