On the generalization of bayesian deep nets for multi-class classification
Paper and Code
Feb 23, 2020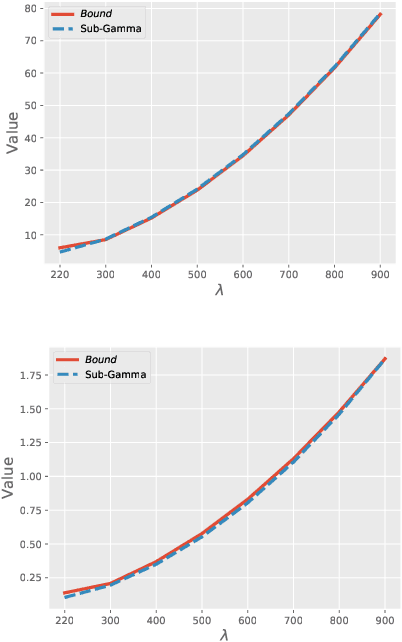
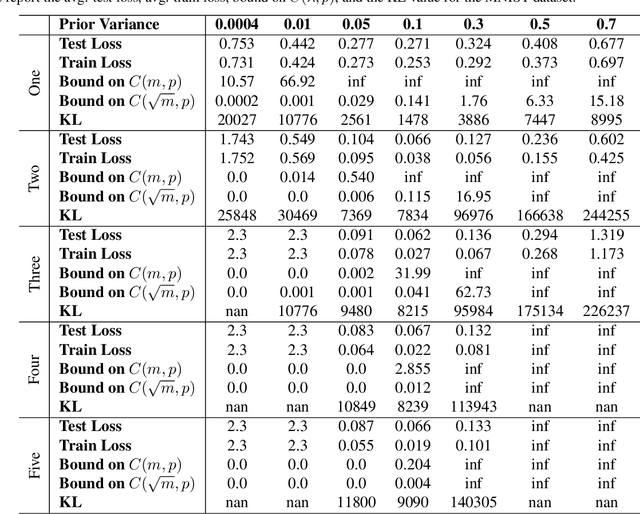
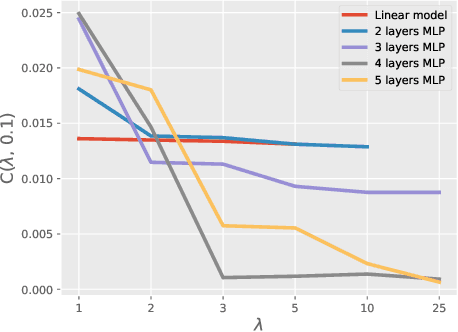
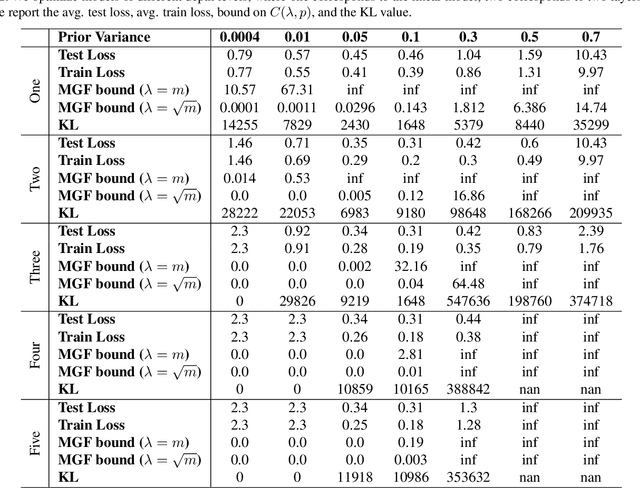
Generalization bounds which assess the difference between the true risk and the empirical risk have been studied extensively. However, to obtain bounds, current techniques use strict assumptions such as a uniformly bounded or a Lipschitz loss function. To avoid these assumptions, in this paper, we propose a new generalization bound for Bayesian deep nets by exploiting the contractivity of the Log-Sobolev inequalities. Using these inequalities adds an additional loss-gradient norm term to the generalization bound, which is intuitively a surrogate of the model complexity. Empirically, we analyze the affect of this loss-gradient norm term using different deep nets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge