Improved Sample Complexity for Global Convergence of Actor-Critic Algorithms
Paper and Code
Oct 11, 2024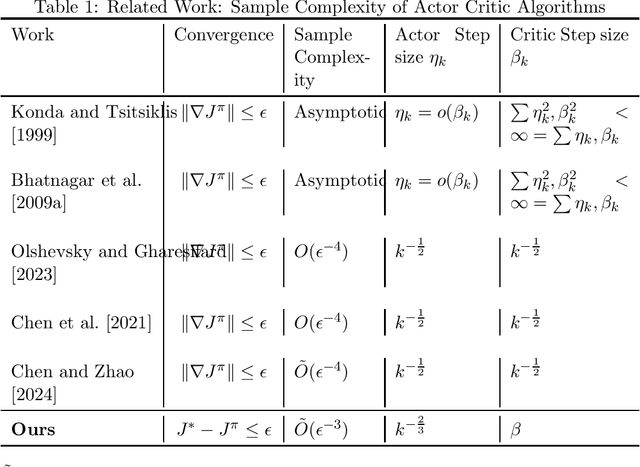
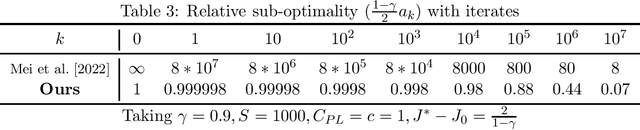
In this paper, we establish the global convergence of the actor-critic algorithm with a significantly improved sample complexity of $O(\epsilon^{-3})$, advancing beyond the existing local convergence results. Previous works provide local convergence guarantees with a sample complexity of $O(\epsilon^{-2})$ for bounding the squared gradient of the return, which translates to a global sample complexity of $O(\epsilon^{-4})$ using the gradient domination lemma. In contrast to traditional methods that employ decreasing step sizes for both the actor and critic, we demonstrate that a constant step size for the critic is sufficient to ensure convergence in expectation. This key insight reveals that using a decreasing step size for the actor alone is sufficient to handle the noise for both the actor and critic. Our findings provide theoretical support for the practical success of many algorithms that rely on constant step sizes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge