An Efficient Solution to s-Rectangular Robust Markov Decision Processes

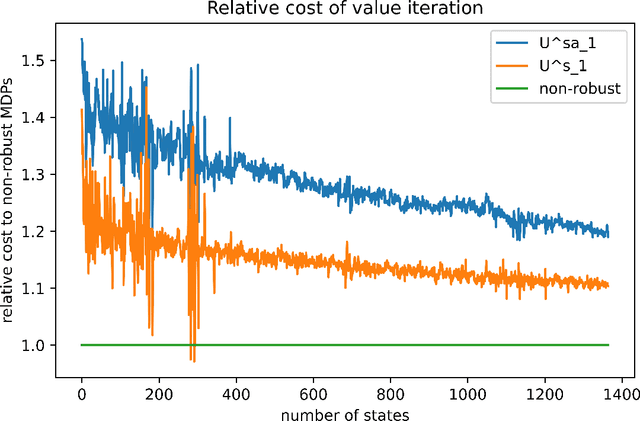
We present an efficient robust value iteration for \texttt{s}-rectangular robust Markov Decision Processes (MDPs) with a time complexity comparable to standard (non-robust) MDPs which is significantly faster than any existing method. We do so by deriving the optimal robust Bellman operator in concrete forms using our $L_p$ water filling lemma. We unveil the exact form of the optimal policies, which turn out to be novel threshold policies with the probability of playing an action proportional to its advantage.