AlignTree: Efficient Defense Against LLM Jailbreak Attacks

Large Language Models (LLMs) are vulnerable to adversarial attacks that bypass safety guidelines and generate harmful content. Mitigating these vulnerabilities requires defense mechanisms that are both robust and computationally efficient. However, existing approaches either incur high computational costs or rely on lightweight defenses that can be easily circumvented, rendering them impractical for real-world LLM-based systems. In this work, we introduce the AlignTree defense, which enhances model alignment while maintaining minimal computational overhead. AlignTree monitors LLM activations during generation and detects misaligned behavior using an efficient random forest classifier. This classifier operates on two signals: (i) the refusal direction -- a linear representation that activates on misaligned prompts, and (ii) an SVM-based signal that captures non-linear features associated with harmful content. Unlike previous methods, AlignTree does not require additional prompts or auxiliary guard models. Through extensive experiments, we demonstrate the efficiency and robustness of AlignTree across multiple LLMs and benchmarks.

Execution Guided Line-by-Line Code Generation

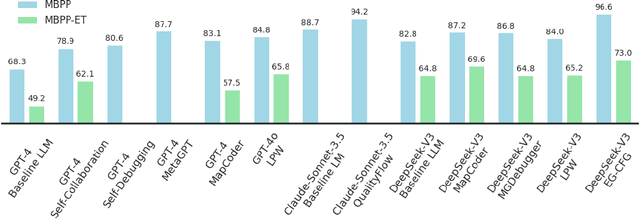
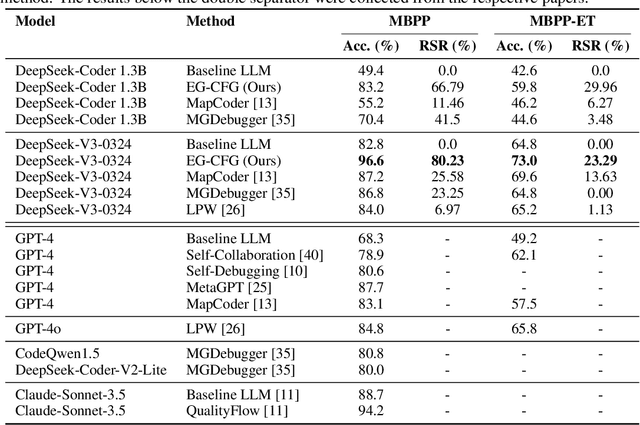
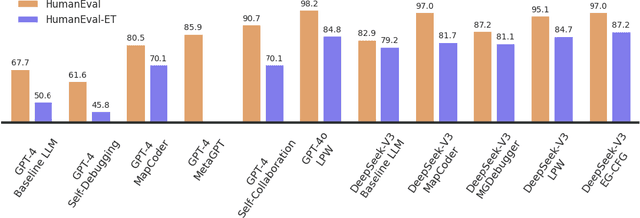
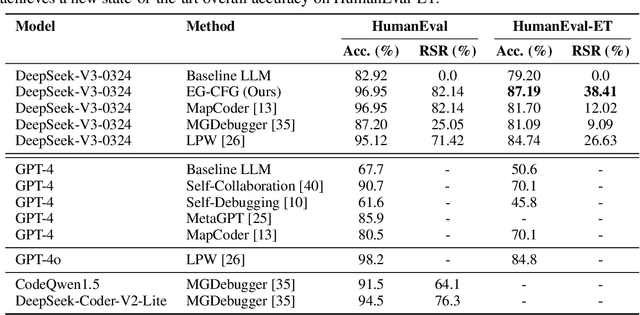
We present a novel approach to neural code generation that incorporates real-time execution signals into the language model generation process. While large language models (LLMs) have demonstrated impressive code generation capabilities, they typically do not utilize execution feedback during inference, a critical signal that human programmers regularly leverage. Our method, Execution-Guided Classifier-Free Guidance (EG-CFG), dynamically incorporates execution signals as the model generates code, providing line-by-line feedback that guides the generation process toward executable solutions. EG-CFG employs a multi-stage process: first, we conduct beam search to sample candidate program completions for each line; second, we extract execution signals by executing these candidates against test cases; and finally, we incorporate these signals into the prompt during generation. By maintaining consistent signals across tokens within the same line and refreshing signals at line boundaries, our approach provides coherent guidance while preserving syntactic structure. Moreover, the method naturally supports native parallelism at the task level in which multiple agents operate in parallel, exploring diverse reasoning paths and collectively generating a broad set of candidate solutions. Our experiments across diverse coding tasks demonstrate that EG-CFG significantly improves code generation performance compared to standard approaches, achieving state-of-the-art results across various levels of complexity, from foundational problems to challenging competitive programming tasks. Our code is available at: https://github.com/boazlavon/eg_cfg

Segment-Based Attention Masking for GPTs

Modern Language Models (LMs) owe much of their success to masked causal attention, the backbone of Generative Pre-Trained Transformer (GPT) models. Although GPTs can process the entire user prompt at once, the causal masking is applied to all input tokens step-by-step, mimicking the generation process. This imposes an unnecessary constraint during the initial "prefill" phase when the model processes the input prompt and generates the internal representations before producing any output tokens. In this work, attention is masked based on the known block structure at the prefill phase, followed by the conventional token-by-token autoregressive process after that. For example, in a typical chat prompt, the system prompt is treated as one block, and the user prompt as the next one. Each of these is treated as a unit for the purpose of masking, such that the first tokens in each block can access the subsequent tokens in a non-causal manner. Then, the model answer is generated in the conventional causal manner. This Segment-by-Segment scheme entails no additional computational overhead. When integrating it into models such as Llama and Qwen, state-of-the-art performance is consistently achieved.

Reversed Attention: On The Gradient Descent Of Attention Layers In GPT

The success of Transformer-based Language Models (LMs) stems from their attention mechanism. While this mechanism has been extensively studied in explainability research, particularly through the attention values obtained during the forward pass of LMs, the backward pass of attention has been largely overlooked. In this work, we study the mathematics of the backward pass of attention, revealing that it implicitly calculates an attention matrix we refer to as "Reversed Attention". We examine the properties of Reversed Attention and demonstrate its ability to elucidate the models' behavior and edit dynamics. In an experimental setup, we showcase the ability of Reversed Attention to directly alter the forward pass of attention, without modifying the model's weights, using a novel method called "attention patching". In addition to enhancing the comprehension of how LM configure attention layers during backpropagation, Reversed Attention maps contribute to a more interpretable backward pass.

Backward Lens: Projecting Language Model Gradients into the Vocabulary Space

Understanding how Transformer-based Language Models (LMs) learn and recall information is a key goal of the deep learning community. Recent interpretability methods project weights and hidden states obtained from the forward pass to the models' vocabularies, helping to uncover how information flows within LMs. In this work, we extend this methodology to LMs' backward pass and gradients. We first prove that a gradient matrix can be cast as a low-rank linear combination of its forward and backward passes' inputs. We then develop methods to project these gradients into vocabulary items and explore the mechanics of how new information is stored in the LMs' neurons.

Interpreting Transformer's Attention Dynamic Memory and Visualizing the Semantic Information Flow of GPT

Recent advances in interpretability suggest we can project weights and hidden states of transformer-based language models (LMs) to their vocabulary, a transformation that makes them human interpretable and enables us to assign semantics to what was seen only as numerical vectors. In this paper, we interpret LM attention heads and memory values, the vectors the models dynamically create and recall while processing a given input. By analyzing the tokens they represent through this projection, we identify patterns in the information flow inside the attention mechanism. Based on these discoveries, we create a tool to visualize a forward pass of Generative Pre-trained Transformers (GPTs) as an interactive flow graph, with nodes representing neurons or hidden states and edges representing the interactions between them. Our visualization simplifies huge amounts of data into easy-to-read plots that reflect why models output their results. We demonstrate the utility of our modeling by identifying the effect LM components have on the intermediate processing in the model before outputting a prediction. For instance, we discover that layer norms are used as semantic filters and find neurons that act as regularization vectors.