Derandomized Novelty Detection with FDR Control via Conformal E-values
Paper and Code
Feb 14, 2023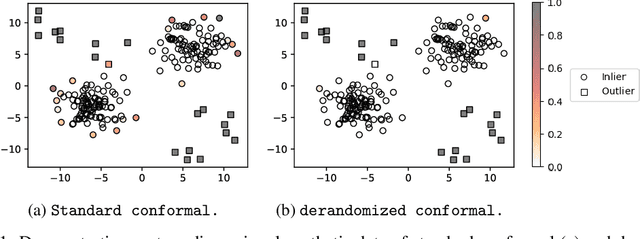
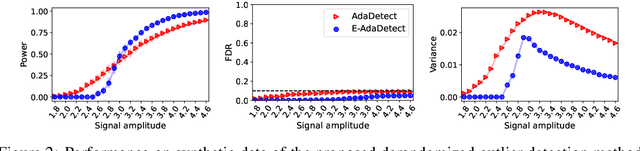
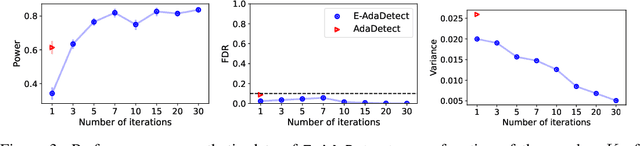
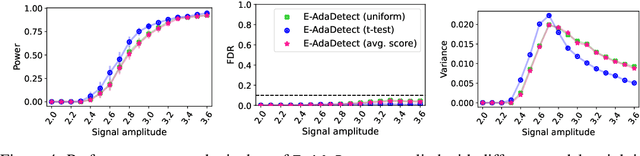
Conformal prediction and other randomized model-free inference techniques are gaining increasing attention as general solutions to rigorously calibrate the output of any machine learning algorithm for novelty detection. This paper contributes to the field by developing a novel method for mitigating their algorithmic randomness, leading to an even more interpretable and reliable framework for powerful novelty detection under false discovery rate control. The idea is to leverage suitable conformal e-values instead of p-values to quantify the significance of each finding, which allows the evidence gathered from multiple mutually dependent analyses of the same data to be seamlessly aggregated. Further, the proposed method can reduce randomness without much loss of power, partly thanks to an innovative way of weighting conformal e-values based on additional side information carefully extracted from the same data. Simulations with synthetic and real data confirm this solution can be effective at eliminating random noise in the inferences obtained with state-of-the-art alternative techniques, sometimes also leading to higher power.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge