funLOCI: a local clustering algorithm for functional data

Nowadays, more and more problems are dealing with data with one infinite continuous dimension: functional data. In this paper, we introduce the funLOCI algorithm which allows to identify functional local clusters or functional loci, i.e., subsets/groups of functions exhibiting similar behaviour across the same continuous subset of the domain. The definition of functional local clusters leverages ideas from multivariate and functional clustering and biclustering and it is based on an additive model which takes into account the shape of the curves. funLOCI is a three-step algorithm based on divisive hierarchical clustering. The use of dendrograms allows to visualize and to guide the searching procedure and the cutting thresholds selection. To deal with the large quantity of local clusters, an extra step is implemented to reduce the number of results to the minimum.

Conformal Prediction Bands for Two-Dimensional Functional Time Series

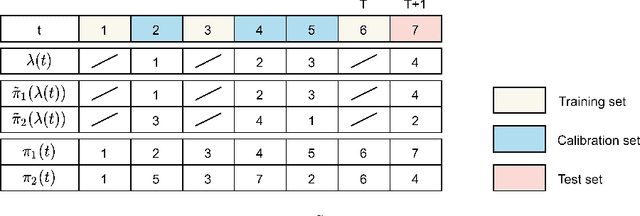
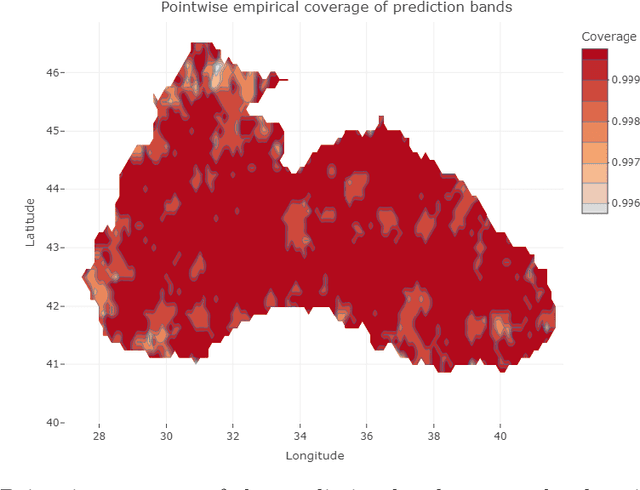
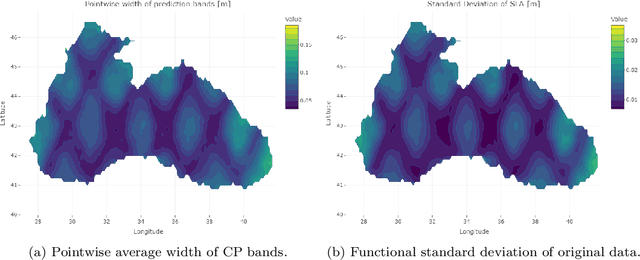
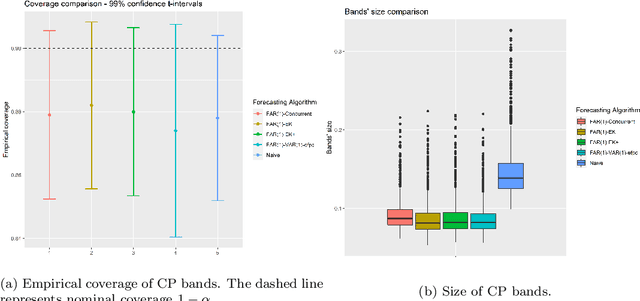
Conformal Prediction (CP) is a versatile nonparametric framework used to quantify uncertainty in prediction problems. In this work, we provide an extension of such method to the case of time series of functions defined on a bivariate domain, by proposing for the first time a distribution-free technique which can be applied to time-evolving surfaces. In order to obtain meaningful and efficient prediction regions, CP must be coupled with an accurate forecasting algorithm, for this reason, we extend the theory of autoregressive processes in Hilbert space in order to allow for functions with a bivariate domain. Given the novelty of the subject, we present estimation techniques for the Functional Autoregressive model (FAR). A simulation study is implemented, in order to investigate how different point predictors affect the resulting prediction bands. Finally, we explore benefits and limits of the proposed approach on a real dataset, collecting daily observations of Sea Level Anomalies of the Black Sea in the last twenty years.

Ridge regression with adaptive additive rectangles and other piecewise functional templates

We propose an $L_{2}$-based penalization algorithm for functional linear regression models, where the coefficient function is shrunk towards a data-driven shape template $\gamma$, which is constrained to belong to a class of piecewise functions by restricting its basis expansion. In particular, we focus on the case where $\gamma$ can be expressed as a sum of $q$ rectangles that are adaptively positioned with respect to the regression error. As the problem of finding the optimal knot placement of a piecewise function is nonconvex, the proposed parametrization allows to reduce the number of variables in the global optimization scheme, resulting in a fitting algorithm that alternates between approximating a suitable template and solving a convex ridge-like problem. The predictive power and interpretability of our method is shown on multiple simulations and two real world case studies.

Measure Inducing Classification and Regression Trees for Functional Data

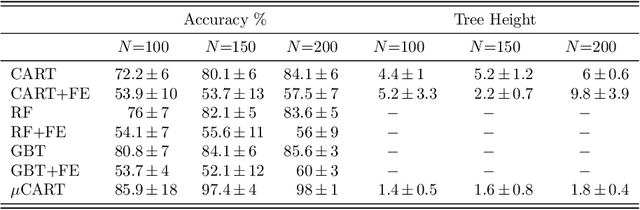
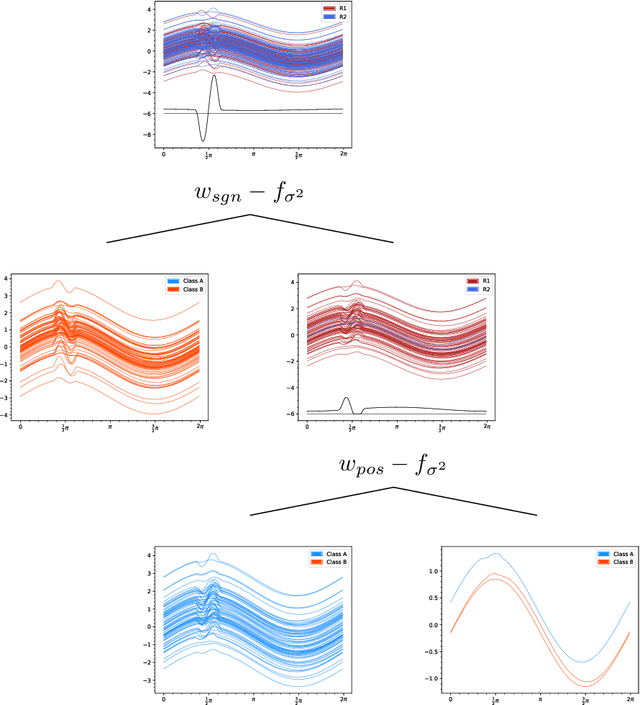
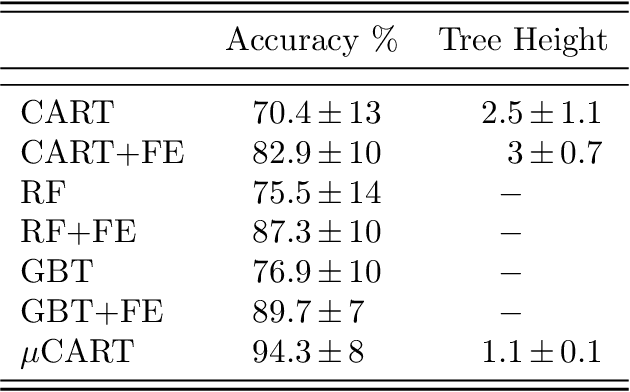
We propose a tree-based algorithm for classification and regression problems in the context of functional data analysis, which allows to leverage representation learning and multiple splitting rules at the node level, reducing generalization error while retaining the interpretability of a tree. This is achieved by learning a weighted functional $L^{2}$ space by means of constrained convex optimization, which is then used to extract multiple weighted integral features from the input functions, in order to determine the binary split for each internal node of the tree. The approach is designed to manage multiple functional inputs and/or outputs, by defining suitable splitting rules and loss functions that can depend on the specific problem and can also be combined with scalar and categorical data, as the tree is grown with the original greedy CART algorithm. We focus on the case of scalar-valued functional inputs defined on unidimensional domains and illustrate the effectiveness of our method in both classification and regression tasks, through a simulation study and four real world applications.

Conformal Prediction: a Unified Review of Theory and New Challenges

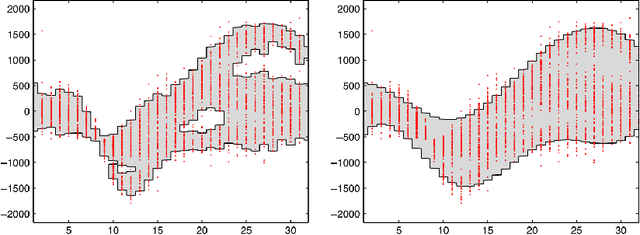
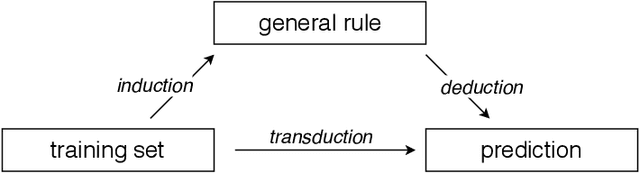
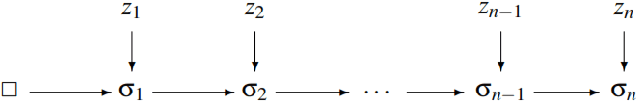
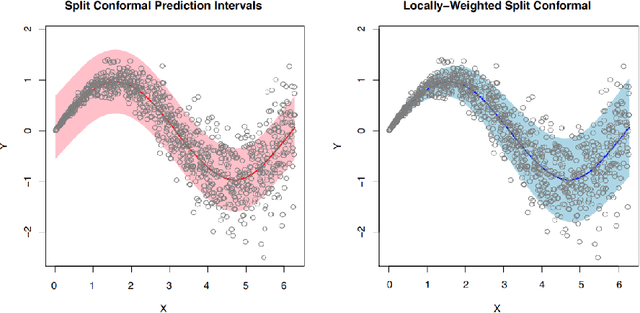
In this work we provide a review of basic ideas and novel developments about Conformal Prediction -- an innovative distribution-free, non-parametric forecasting method, based on minimal assumptions -- that is able to yield in a very straightforward way predictions sets that are valid in a statistical sense also in in the finite sample case. The in-depth discussion provided in the paper covers the theoretical underpinnings of Conformal Prediction, and then proceeds to list the more advanced developments and adaptations of the original idea.