Edoardo Belli
Ridge regression with adaptive additive rectangles and other piecewise functional templates
Nov 02, 2020



Abstract:We propose an $L_{2}$-based penalization algorithm for functional linear regression models, where the coefficient function is shrunk towards a data-driven shape template $\gamma$, which is constrained to belong to a class of piecewise functions by restricting its basis expansion. In particular, we focus on the case where $\gamma$ can be expressed as a sum of $q$ rectangles that are adaptively positioned with respect to the regression error. As the problem of finding the optimal knot placement of a piecewise function is nonconvex, the proposed parametrization allows to reduce the number of variables in the global optimization scheme, resulting in a fitting algorithm that alternates between approximating a suitable template and solving a convex ridge-like problem. The predictive power and interpretability of our method is shown on multiple simulations and two real world case studies.
Smoothly Adaptively Centered Ridge Estimator
Oct 31, 2020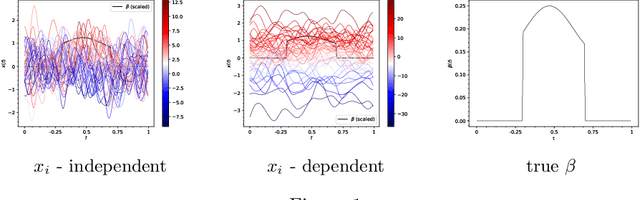



Abstract:With a focus on linear models with smooth functional covariates, we propose a penalization framework (SACR) based on the nonzero centered ridge, where the center of the penalty is optimally reweighted in a supervised way, starting from the ordinary ridge solution as the initial centerfunction. In particular, we introduce a convex formulation that jointly estimates the model's coefficients and the weight function, with a roughness penalty on the centerfunction and constraints on the weights in order to recover a possibly smooth and/or sparse solution. This allows for a non-iterative and continuous variable selection mechanism, as the weight function can either inflate or deflate the initial center, in order to target the penalty towards a suitable center, with the objective to reduce the unwanted shrinkage on the nonzero coefficients, instead of uniformly shrinking the whole coefficient function. As empirical evidence of the interpretability and predictive power of our method, we provide a simulation study and two real world spectroscopy applications with both classification and regression.
Measure Inducing Classification and Regression Trees for Functional Data
Oct 30, 2020
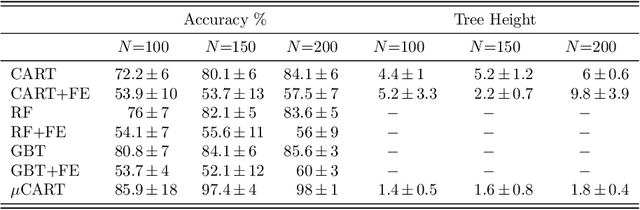
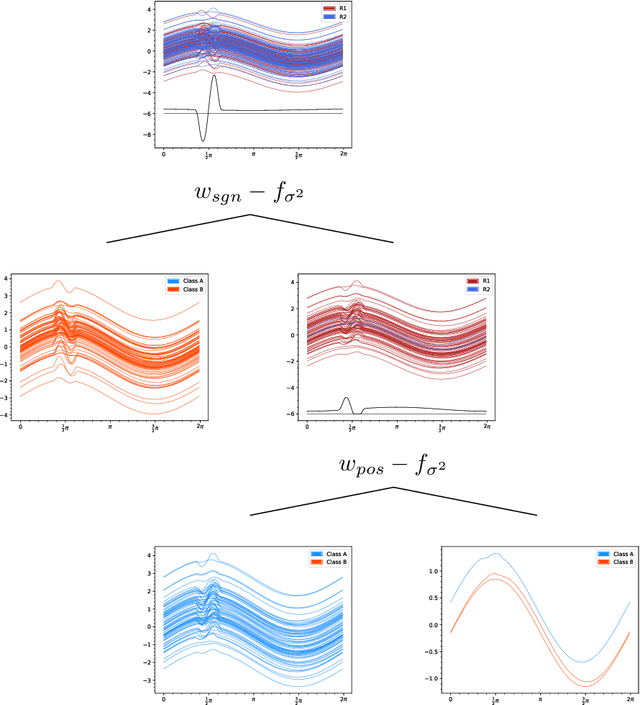
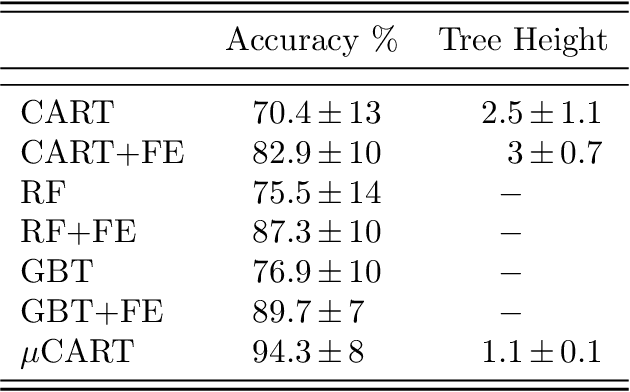
Abstract:We propose a tree-based algorithm for classification and regression problems in the context of functional data analysis, which allows to leverage representation learning and multiple splitting rules at the node level, reducing generalization error while retaining the interpretability of a tree. This is achieved by learning a weighted functional $L^{2}$ space by means of constrained convex optimization, which is then used to extract multiple weighted integral features from the input functions, in order to determine the binary split for each internal node of the tree. The approach is designed to manage multiple functional inputs and/or outputs, by defining suitable splitting rules and loss functions that can depend on the specific problem and can also be combined with scalar and categorical data, as the tree is grown with the original greedy CART algorithm. We focus on the case of scalar-valued functional inputs defined on unidimensional domains and illustrate the effectiveness of our method in both classification and regression tasks, through a simulation study and four real world applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge