Introducing Diminutive Causal Structure into Graph Representation Learning

When engaging in end-to-end graph representation learning with Graph Neural Networks (GNNs), the intricate causal relationships and rules inherent in graph data pose a formidable challenge for the model in accurately capturing authentic data relationships. A proposed mitigating strategy involves the direct integration of rules or relationships corresponding to the graph data into the model. However, within the domain of graph representation learning, the inherent complexity of graph data obstructs the derivation of a comprehensive causal structure that encapsulates universal rules or relationships governing the entire dataset. Instead, only specialized diminutive causal structures, delineating specific causal relationships within constrained subsets of graph data, emerge as discernible. Motivated by empirical insights, it is observed that GNN models exhibit a tendency to converge towards such specialized causal structures during the training process. Consequently, we posit that the introduction of these specific causal structures is advantageous for the training of GNN models. Building upon this proposition, we introduce a novel method that enables GNN models to glean insights from these specialized diminutive causal structures, thereby enhancing overall performance. Our method specifically extracts causal knowledge from the model representation of these diminutive causal structures and incorporates interchange intervention to optimize the learning process. Theoretical analysis serves to corroborate the efficacy of our proposed method. Furthermore, empirical experiments consistently demonstrate significant performance improvements across diverse datasets.

BayesPrompt: Prompting Large-Scale Pre-Trained Language Models on Few-shot Inference via Debiased Domain Abstraction

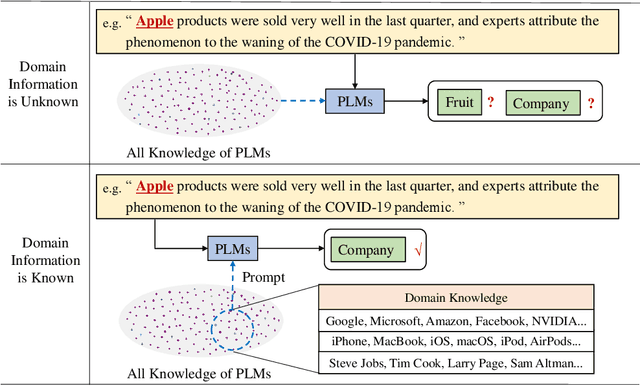
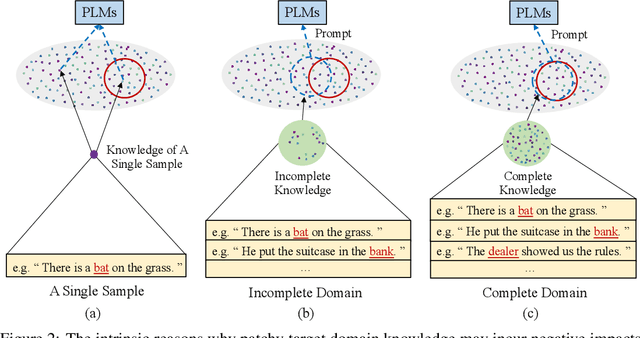
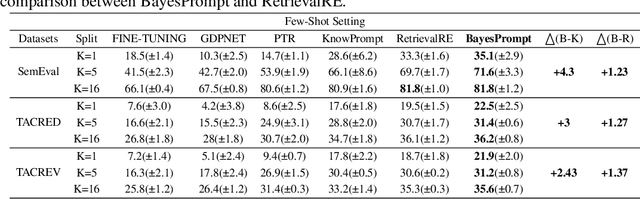
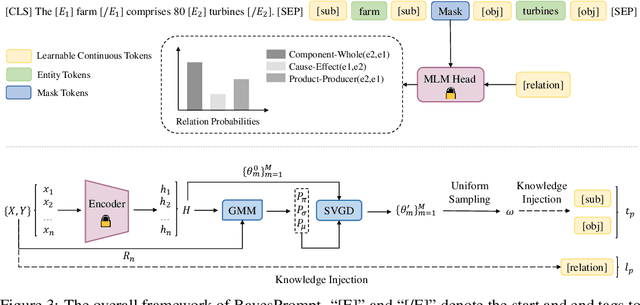
As a novel and effective fine-tuning paradigm based on large-scale pre-trained language models (PLMs), prompt-tuning aims to reduce the gap between downstream tasks and pre-training objectives. While prompt-tuning has yielded continuous advancements in various tasks, such an approach still remains a persistent defect: prompt-tuning methods fail to generalize to specific few-shot patterns. From the perspective of distribution analyses, we disclose that the intrinsic issues behind the phenomenon are the over-multitudinous conceptual knowledge contained in PLMs and the abridged knowledge for target downstream domains, which jointly result in that PLMs mis-locate the knowledge distributions corresponding to the target domains in the universal knowledge embedding space. To this end, we intuitively explore to approximate the unabridged target domains of downstream tasks in a debiased manner, and then abstract such domains to generate discriminative prompts, thereby providing the de-ambiguous guidance for PLMs. Guided by such an intuition, we propose a simple yet effective approach, namely BayesPrompt, to learn prompts that contain the domain discriminative information against the interference from domain-irrelevant knowledge. BayesPrompt primitively leverages known distributions to approximate the debiased factual distributions of target domains and further uniformly samples certain representative features from the approximated distributions to generate the ultimate prompts for PLMs. We provide theoretical insights with the connection to domain adaptation. Empirically, our method achieves state-of-the-art performance on benchmarks.

Hierarchical Topology Isomorphism Expertise Embedded Graph Contrastive Learning

Graph contrastive learning (GCL) aims to align the positive features while differentiating the negative features in the latent space by minimizing a pair-wise contrastive loss. As the embodiment of an outstanding discriminative unsupervised graph representation learning approach, GCL achieves impressive successes in various graph benchmarks. However, such an approach falls short of recognizing the topology isomorphism of graphs, resulting in that graphs with relatively homogeneous node features cannot be sufficiently discriminated. By revisiting classic graph topology recognition works, we disclose that the corresponding expertise intuitively complements GCL methods. To this end, we propose a novel hierarchical topology isomorphism expertise embedded graph contrastive learning, which introduces knowledge distillations to empower GCL models to learn the hierarchical topology isomorphism expertise, including the graph-tier and subgraph-tier. On top of this, the proposed method holds the feature of plug-and-play, and we empirically demonstrate that the proposed method is universal to multiple state-of-the-art GCL models. The solid theoretical analyses are further provided to prove that compared with conventional GCL methods, our method acquires the tighter upper bound of Bayes classification error. We conduct extensive experiments on real-world benchmarks to exhibit the performance superiority of our method over candidate GCL methods, e.g., for the real-world graph representation learning experiments, the proposed method beats the state-of-the-art method by 0.23% on unsupervised representation learning setting, 0.43% on transfer learning setting. Our code is available at https://github.com/jyf123/HTML.

Rethinking Causal Relationships Learning in Graph Neural Networks

Graph Neural Networks (GNNs) demonstrate their significance by effectively modeling complex interrelationships within graph-structured data. To enhance the credibility and robustness of GNNs, it becomes exceptionally crucial to bolster their ability to capture causal relationships. However, despite recent advancements that have indeed strengthened GNNs from a causal learning perspective, conducting an in-depth analysis specifically targeting the causal modeling prowess of GNNs remains an unresolved issue. In order to comprehensively analyze various GNN models from a causal learning perspective, we constructed an artificially synthesized dataset with known and controllable causal relationships between data and labels. The rationality of the generated data is further ensured through theoretical foundations. Drawing insights from analyses conducted using our dataset, we introduce a lightweight and highly adaptable GNN module designed to strengthen GNNs' causal learning capabilities across a diverse range of tasks. Through a series of experiments conducted on both synthetic datasets and other real-world datasets, we empirically validate the effectiveness of the proposed module.

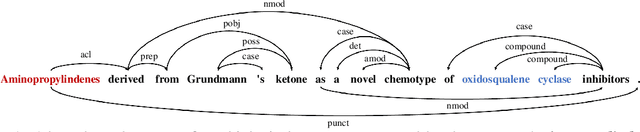
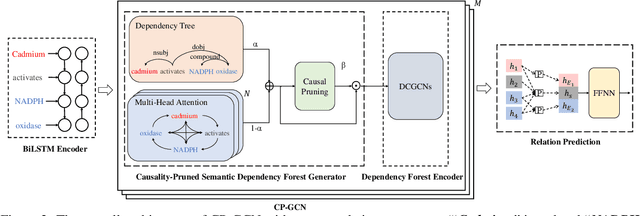
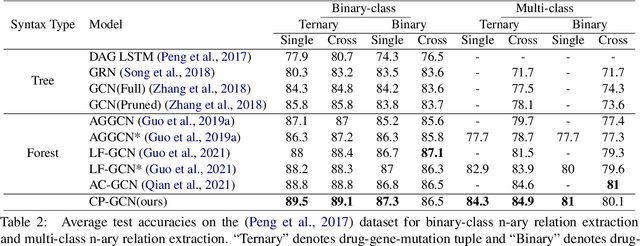
Supporting Medical Relation Extraction via Causality-Pruned Semantic Dependency Forest

Medical Relation Extraction (MRE) task aims to extract relations between entities in medical texts. Traditional relation extraction methods achieve impressive success by exploring the syntactic information, e.g., dependency tree. However, the quality of the 1-best dependency tree for medical texts produced by an out-of-domain parser is relatively limited so that the performance of medical relation extraction method may degenerate. To this end, we propose a method to jointly model semantic and syntactic information from medical texts based on causal explanation theory. We generate dependency forests consisting of the semantic-embedded 1-best dependency tree. Then, a task-specific causal explainer is adopted to prune the dependency forests, which are further fed into a designed graph convolutional network to learn the corresponding representation for downstream task. Empirically, the various comparisons on benchmark medical datasets demonstrate the effectiveness of our model.

An SBR Based Ray Tracing Channel Modeling Method for THz and Massive MIMO Communications

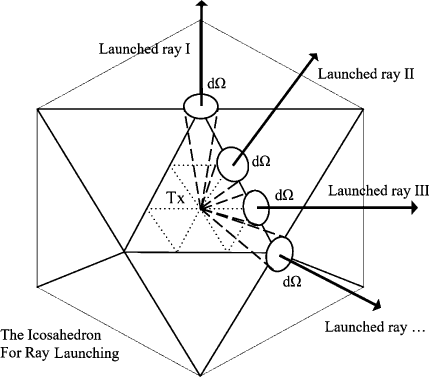
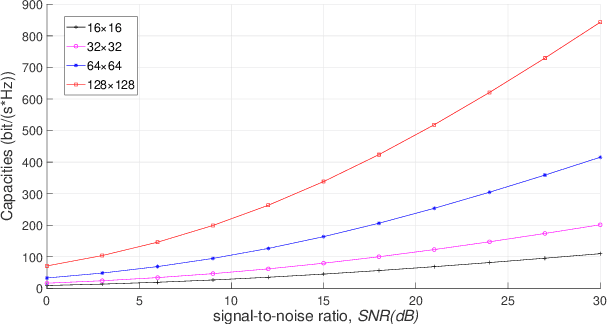
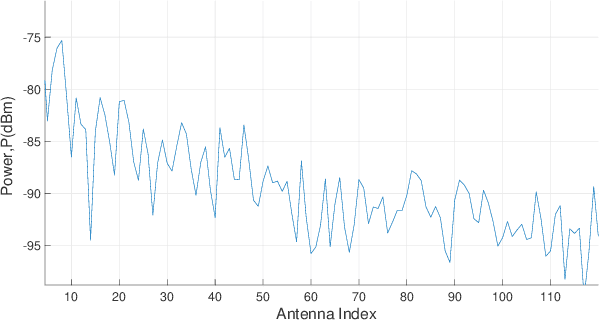
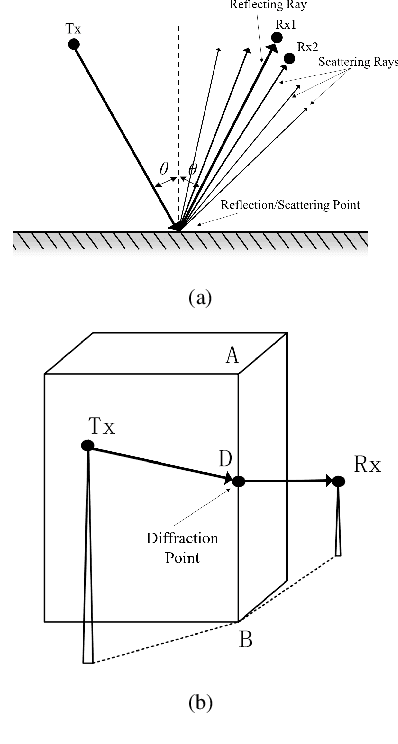
Terahertz (THz) communication and the application of massive multiple-input multiple-output (MIMO) technology have been proved significant for the sixth generation (6G) communication systems, and have gained global interests. In this paper, we employ the shooting and bouncing ray (SBR) method integrated with acceleration technology to model THz and massive MIMO channel. The results of ray tracing (RT) simulation in this paper, i.e., angle of departure (AoD), angle of arrival (AoA), and power delay profile (PDP) under the frequency band supported by the commercial RT software Wireless Insite (WI) are in agreement with those produced by WI. Based on the Kirchhoff scattering effect on material surfaces and atmospheric absorption loss showing at THz frequency band, the modified propagation models of Fresnel reflection coefficients and free-space attenuation are consistent with the measured results. For massive MIMO, the channel capacity and the stochastic power distribution are analyzed. The results indicate the applicability of SBR method for building deterministic models of THz and massive MIMO channels with extensive functions and acceptable accuracy.

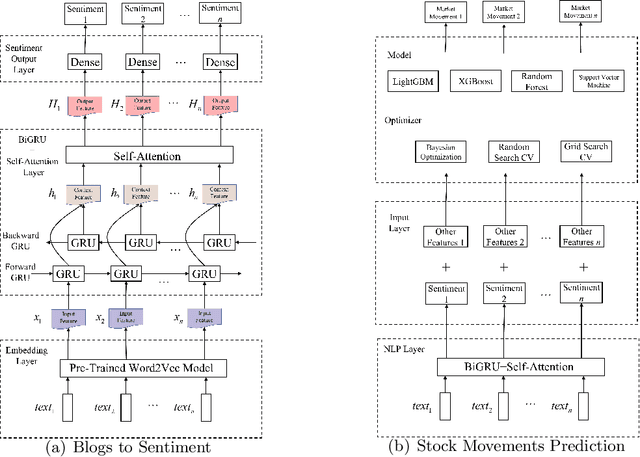
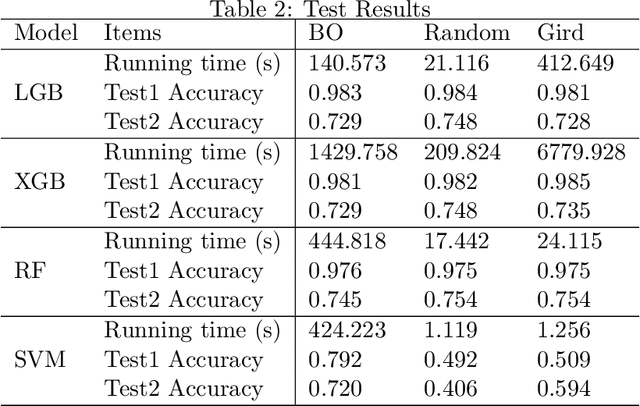
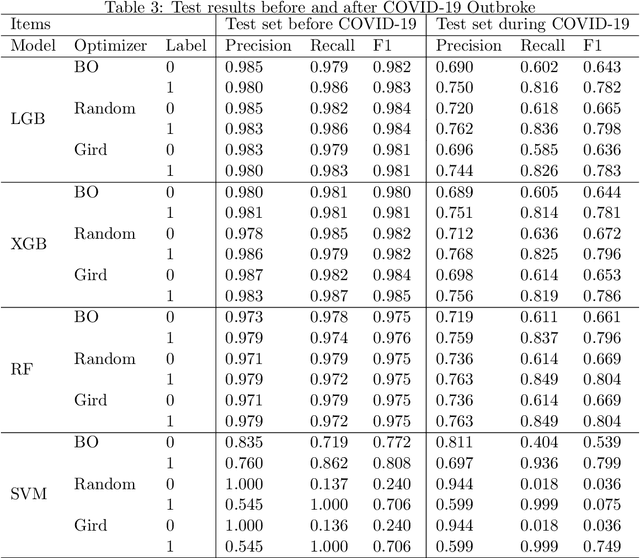
AlphaMLDigger: A Novel Machine Learning Solution to Explore Excess Return on Investment

How to quickly and automatically mine effective information and serve investment decisions has attracted more and more attention from academia and industry. And new challenges have been raised with the global pandemic. This paper proposes a two-phase AlphaMLDigger that effectively finds excessive returns in the highly fluctuated market. In phase 1, a deep sequential NLP model is proposed to transfer blogs on Sina Microblog to market sentiment. In phase 2, the predicted market sentiment is combined with social network indicator features and stock market history features to predict the stock movements with different Machine Learning models and optimizers. The results show that our AlphaMLDigger achieves higher accuracy in the test set than previous works and is robust to the negative impact of COVID-19 to some extent.

Convergence of Contrastive Divergence Algorithm in Exponential Family

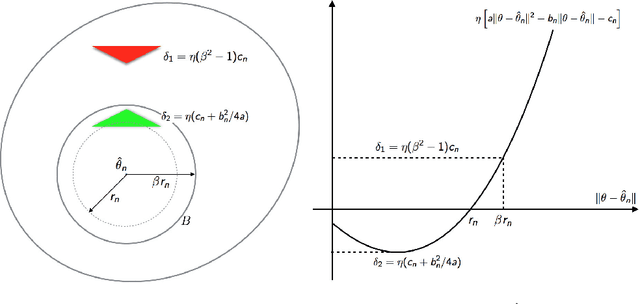
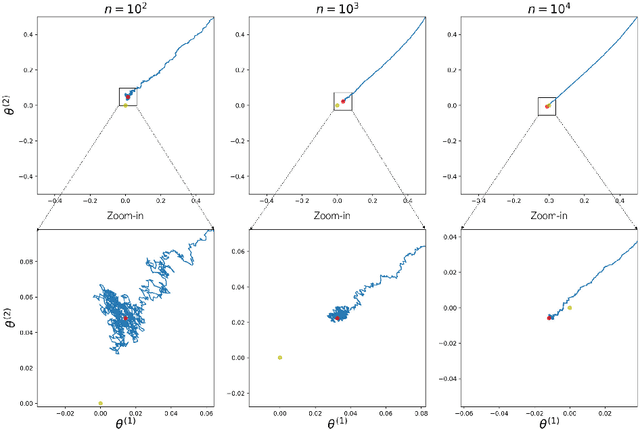
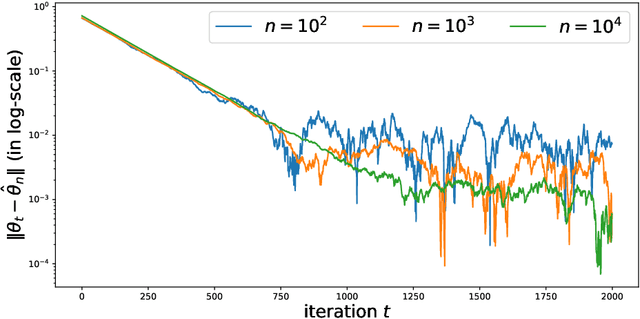
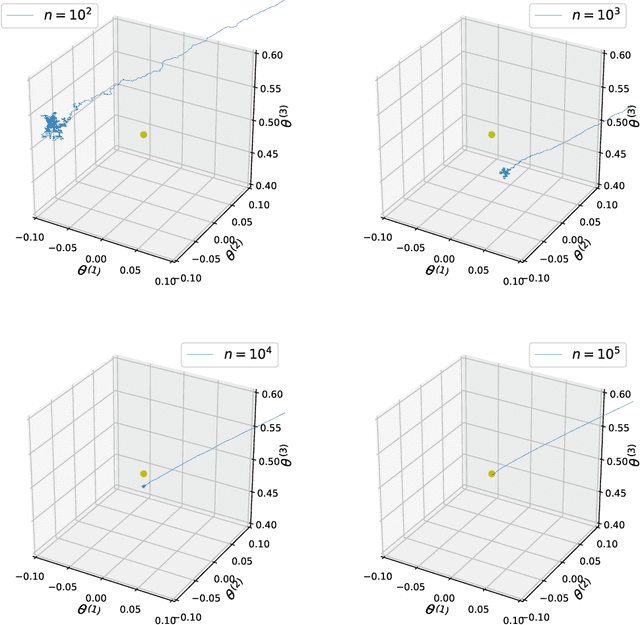
The Contrastive Divergence (CD) algorithm has achieved notable success in training energy-based models including Restricted Boltzmann Machines and played a key role in the emergence of deep learning. The idea of this algorithm is to approximate the intractable term in the exact gradient of the log-likelihood function by using short Markov chain Monte Carlo (MCMC) runs. The approximate gradient is computationally-cheap but biased. Whether and why the CD algorithm provides an asymptotically consistent estimate are still open questions. This paper studies the asymptotic properties of the CD algorithm in canonical exponential families, which are special cases of the energy-based model. Suppose the CD algorithm runs $m$ MCMC transition steps at each iteration $t$ and iteratively generates a sequence of parameter estimates $\{\theta_t\}_{t \ge 0}$ given an i.i.d. data sample $\{X_i\}_{i=1}^n \sim p_{\theta_\star}$. Under conditions which are commonly obeyed by the CD algorithm in practice, we prove the existence of some bounded $m$ such that any limit point of the time average $\left. \sum_{s=0}^{t-1} \theta_s \right/ t$ as $t \to \infty$ is a consistent estimate for the true parameter $\theta_\star$. Our proof is based on the fact that $\{\theta_t\}_{t \ge 0}$ is a homogenous Markov chain conditional on the data sample $\{X_i\}_{i=1}^n$. This chain meets the Foster-Lyapunov drift criterion and converges to a random walk around the Maximum Likelihood Estimate. The range of the random walk shrinks to zero at rate $\mathcal{O}(1/\sqrt[3]{n})$ as the sample size $n \to \infty$.