Estimating mutual information in high dimensions via classification error
Paper and Code
Oct 10, 2016
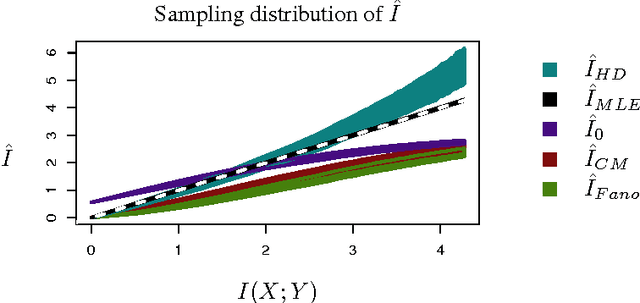
Multivariate pattern analyses approaches in neuroimaging are fundamentally concerned with investigating the quantity and type of information processed by various regions of the human brain; typically, estimates of classification accuracy are used to quantify information. While a extensive and powerful library of methods can be applied to train and assess classifiers, it is not always clear how to use the resulting measures of classification performance to draw scientific conclusions: e.g. for the purpose of evaluating redundancy between brain regions. An additional confound for interpreting classification performance is the dependence of the error rate on the number and choice of distinct classes obtained for the classification task. In contrast, mutual information is a quantity defined independently of the experimental design, and has ideal properties for comparative analyses. Unfortunately, estimating the mutual information based on observations becomes statistically infeasible in high dimensions without some kind of assumption or prior. In this paper, we construct a novel classification-based estimator of mutual information based on high-dimensional asymptotics. We show that in a particular limiting regime, the mutual information is an invertible function of the expected $k$-class Bayes error. While the theory is based on a large-sample, high-dimensional limit, we demonstrate through simulations that our proposed estimator has superior performance to the alternatives in problems of moderate dimensionality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge