Towards Interpretable Deep Generative Models via Causal Representation Learning

Recent developments in generative artificial intelligence (AI) rely on machine learning techniques such as deep learning and generative modeling to achieve state-of-the-art performance across wide-ranging domains. These methods' surprising performance is due in part to their ability to learn implicit "representations'' of complex, multi-modal data. Unfortunately, deep neural networks are notoriously black boxes that obscure these representations, making them difficult to interpret or analyze. To resolve these difficulties, one approach is to build new interpretable neural network models from the ground up. This is the goal of the emerging field of causal representation learning (CRL) that uses causality as a vector for building flexible, interpretable, and transferable generative AI. CRL can be seen as a culmination of three intrinsically statistical problems: (i) latent variable models such as factor analysis; (ii) causal graphical models with latent variables; and (iii) nonparametric statistics and deep learning. This paper reviews recent progress in CRL from a statistical perspective, focusing on connections to classical models and statistical and causal identifiablity results. This review also highlights key application areas, implementation strategies, and open statistical questions in CRL.

Identifiable Variational Autoencoders via Sparse Decoding

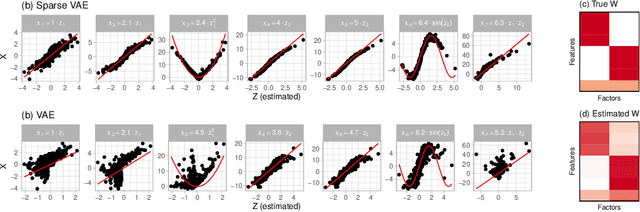
We develop the Sparse VAE, a deep generative model for unsupervised representation learning on high-dimensional data. Given a dataset of observations, the Sparse VAE learns a set of latent factors that captures its distribution. The model is sparse in the sense that each feature of the dataset (i.e., each dimension) depends on a small subset of the latent factors. As examples, in ratings data each movie is only described by a few genres; in text data each word is only applicable to a few topics; in genomics, each gene is active in only a few biological processes. We first show that the Sparse VAE is identifiable: given data drawn from the model, there exists a uniquely optimal set of factors. (In contrast, most VAE-based models are not identifiable.) The key assumption behind Sparse-VAE identifiability is the existence of "anchor features", where for each factor there exists a feature that depends only on that factor. Importantly, the anchor features do not need to be known in advance. We then show how to fit the Sparse VAE with variational EM. Finally, we empirically study the Sparse VAE with both simulated and real data. We find that it recovers meaningful latent factors and has smaller heldout reconstruction error than related methods.