VIGN: Variational Integrator Graph Networks

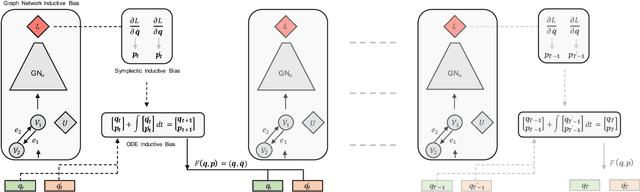
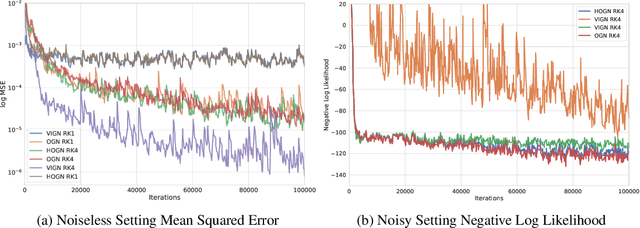
Rich, physically-informed inductive biases play an imperative role in accurately modelling the time dynamics of physical systems. In this paper, we introduce Variational Integrator Graph Networks (VIGNs), the first approach to combine a Variational Integrator (VI) inductive bias with a Graph Network (GN) and demonstrate an order of magnitude improvement in performance, both in terms of data-efficient learning and predictive accuracy, over existing methods. We show that this improvement arises because VIs induce coupled learning of generalized position and momentum updates which can be formulated as a Partitioned Runge-Kutta (PRK) method. We empirically establish that VIGN outperforms numerous methods in learning from existing datasets with noise.