First principles physics-informed neural network for quantum wavefunctions and eigenvalue surfaces

Physics-informed neural networks have been widely applied to learn general parametric solutions of differential equations. Here, we propose a neural network to discover parametric eigenvalue and eigenfunction surfaces of quantum systems. We apply our method to solve the hydrogen molecular ion. This is an ab-initio deep learning method that solves the Schrodinger equation with the Coulomb potential yielding realistic wavefunctions that include a cusp at the ion positions. The neural solutions are continuous and differentiable functions of the interatomic distance and their derivatives are analytically calculated by applying automatic differentiation. Such a parametric and analytical form of the solutions is useful for further calculations such as the determination of force fields.

Modeling the effect of the vaccination campaign on the Covid-19 pandemic

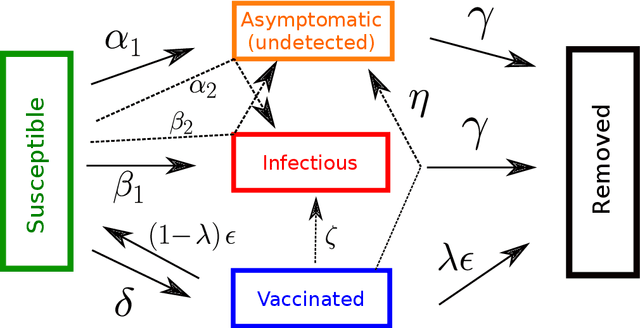
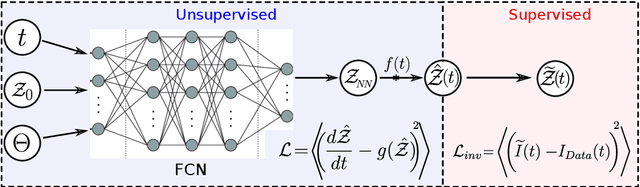
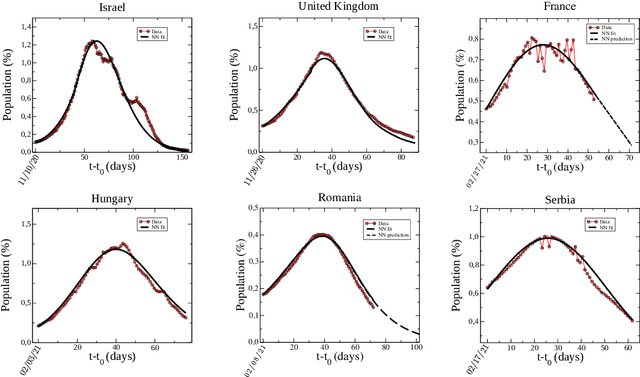
Population-wide vaccination is critical for containing the SARS-CoV-2 (Covid-19) pandemic when combined with restrictive and prevention measures. In this study, we introduce SAIVR, a mathematical model able to forecast the Covid-19 epidemic evolution during the vaccination campaign. SAIVR extends the widely used Susceptible-Infectious-Removed (SIR) model by considering the Asymptomatic (A) and Vaccinated (V) compartments. The model contains several parameters and initial conditions that are estimated by employing a semi-supervised machine learning procedure. After training an unsupervised neural network to solve the SAIVR differential equations, a supervised framework then estimates the optimal conditions and parameters that best fit recent infectious curves of 27 countries. Instructed by these results, we performed an extensive study on the temporal evolution of the pandemic under varying values of roll-out daily rates, vaccine efficacy, and a broad range of societal vaccine hesitancy/denial levels. The concept of herd immunity is questioned by studying future scenarios which involve different vaccination efforts and more infectious Covid-19 variants.