Henry Jin
Physics-Informed Neural Networks for Quantum Eigenvalue Problems
Feb 24, 2022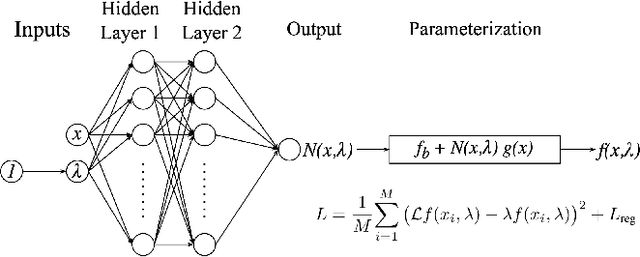
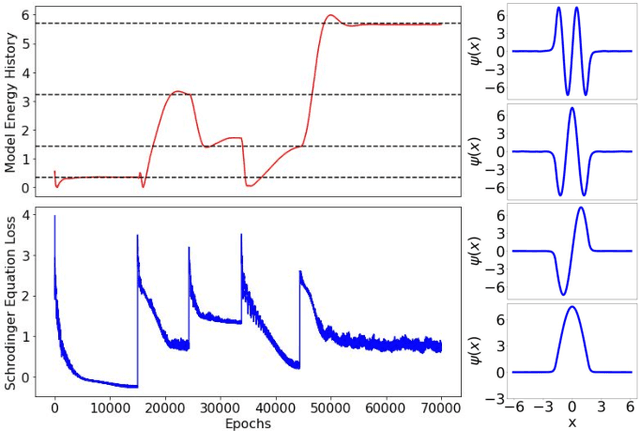
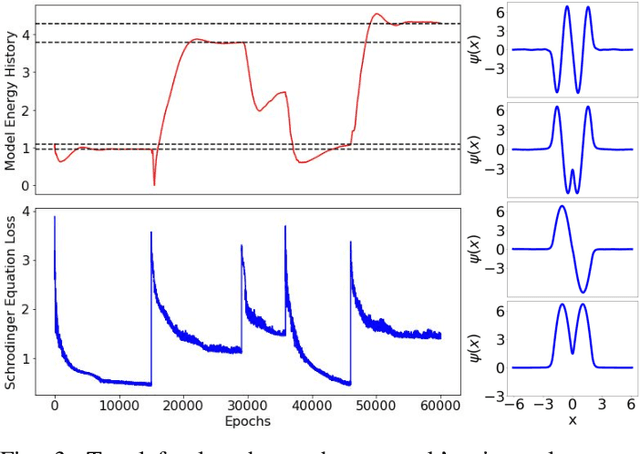
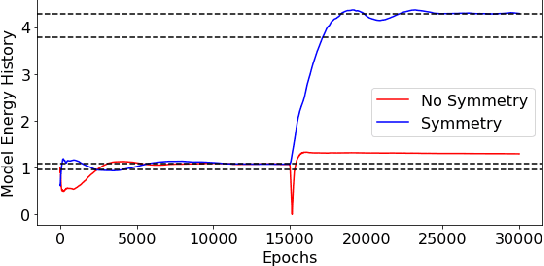
Abstract:Eigenvalue problems are critical to several fields of science and engineering. We expand on the method of using unsupervised neural networks for discovering eigenfunctions and eigenvalues for differential eigenvalue problems. The obtained solutions are given in an analytical and differentiable form that identically satisfies the desired boundary conditions. The network optimization is data-free and depends solely on the predictions of the neural network. We introduce two physics-informed loss functions. The first, called ortho-loss, motivates the network to discover pair-wise orthogonal eigenfunctions. The second loss term, called norm-loss, requests the discovery of normalized eigenfunctions and is used to avoid trivial solutions. We find that embedding even or odd symmetries to the neural network architecture further improves the convergence for relevant problems. Lastly, a patience condition can be used to automatically recognize eigenfunction solutions. This proposed unsupervised learning method is used to solve the finite well, multiple finite wells, and hydrogen atom eigenvalue quantum problems.
Unsupervised Neural Networks for Quantum Eigenvalue Problems
Oct 10, 2020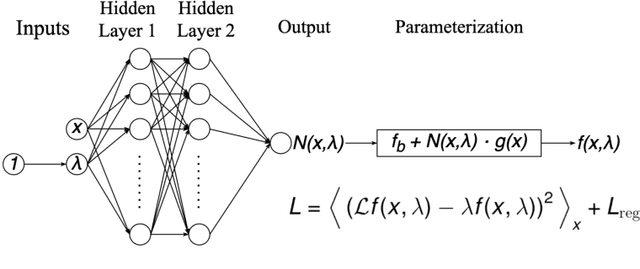
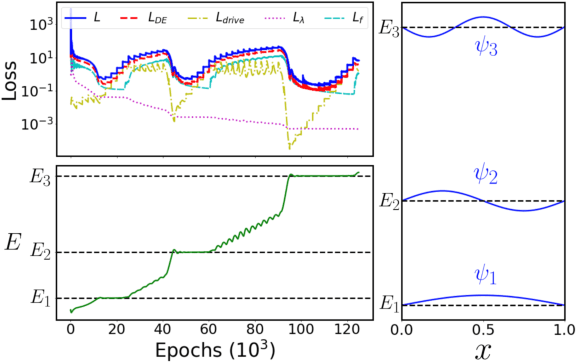
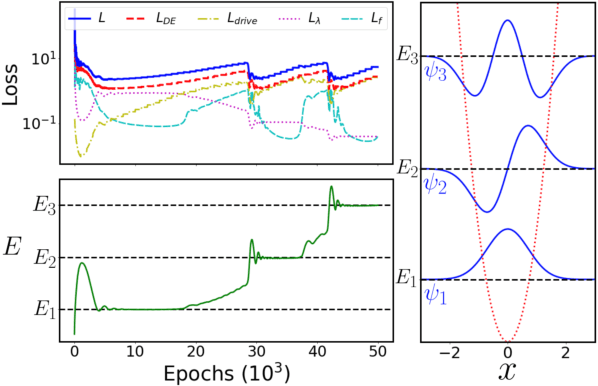
Abstract:Eigenvalue problems are critical to several fields of science and engineering. We present a novel unsupervised neural network for discovering eigenfunctions and eigenvalues for differential eigenvalue problems with solutions that identically satisfy the boundary conditions. A scanning mechanism is embedded allowing the method to find an arbitrary number of solutions. The network optimization is data-free and depends solely on the predictions. The unsupervised method is used to solve the quantum infinite well and quantum oscillator eigenvalue problems.
NBDT: Neural-Backed Decision Trees
Apr 01, 2020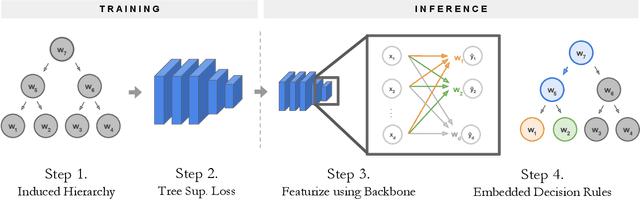
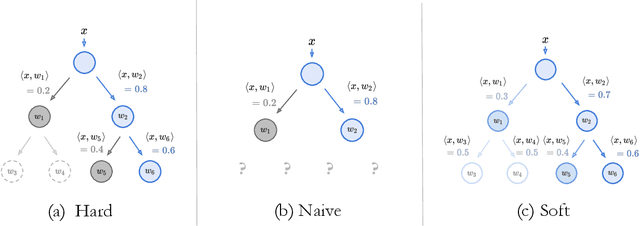
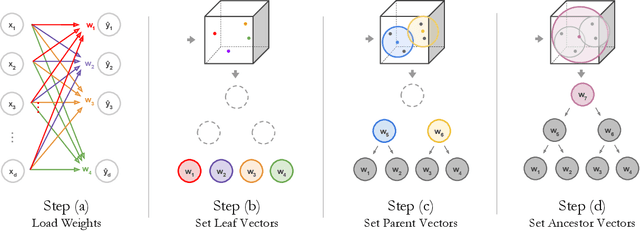

Abstract:Deep learning is being adopted in settings where accurate and justifiable predictions are required, ranging from finance to medical imaging. While there has been recent work providing post-hoc explanations for model predictions, there has been relatively little work exploring more directly interpretable models that can match state-of-the-art accuracy. Historically, decision trees have been the gold standard in balancing interpretability and accuracy. However, recent attempts to combine decision trees with deep learning have resulted in models that (1) achieve accuracies far lower than that of modern neural networks (e.g. ResNet) even on small datasets (e.g. MNIST), and (2) require significantly different architectures, forcing practitioners pick between accuracy and interpretability. We forgo this dilemma by creating Neural-Backed Decision Trees (NBDTs) that (1) achieve neural network accuracy and (2) require no architectural changes to a neural network. NBDTs achieve accuracy within 1% of the base neural network on CIFAR10, CIFAR100, TinyImageNet, using recently state-of-the-art WideResNet; and within 2% of EfficientNet on ImageNet. This yields state-of-the-art explainable models on ImageNet, with NBDTs improving the baseline by ~14% to 75.30% top-1 accuracy. Furthermore, we show interpretability of our model's decisions both qualitatively and quantitatively via a semi-automatic process. Code and pretrained NBDTs can be found at https://github.com/alvinwan/neural-backed-decision-trees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge