Universality of Deep Neural Network Lottery Tickets: A Renormalization Group Perspective

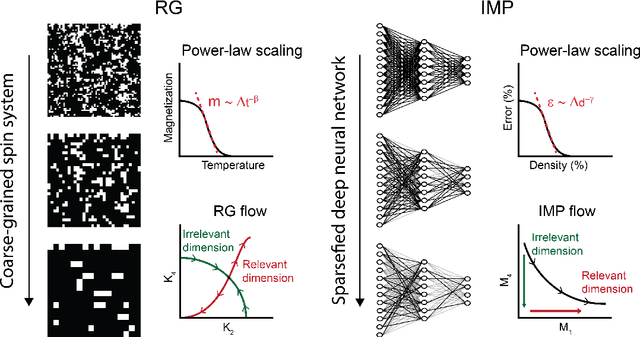
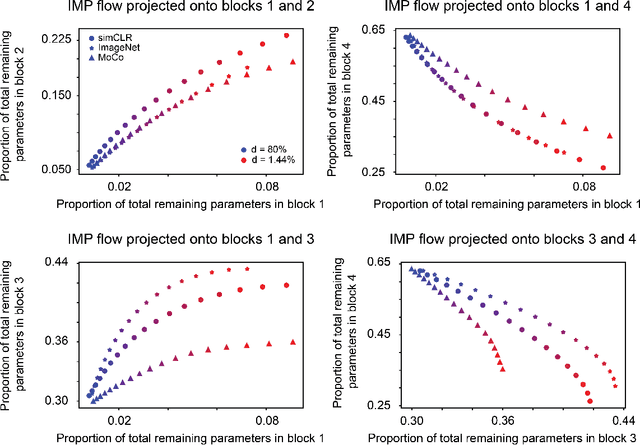
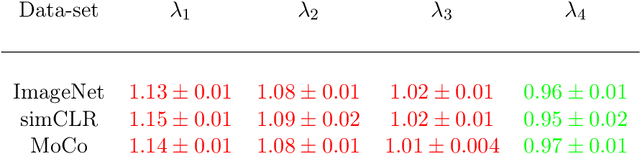
Foundational work on the Lottery Ticket Hypothesis has suggested an exciting corollary: winning tickets found in the context of one task can be transferred to similar tasks, possibly even across different architectures. While this has become of broad practical and theoretical interest, to date, there exists no detailed understanding of why winning ticket universality exists, or any way of knowing \textit{a priori} whether a given ticket can be transferred to a given task. To address these outstanding open questions, we make use of renormalization group theory, one of the most successful tools in theoretical physics. We find that iterative magnitude pruning, the method used for discovering winning tickets, is a renormalization group scheme. This opens the door to a wealth of existing numerical and theoretical tools, some of which we leverage here to examine winning ticket universality in large scale lottery ticket experiments, as well as sheds new light on the success iterative magnitude pruning has found in the field of sparse machine learning.