Data-driven emergence of convolutional structure in neural networks
Paper and Code
Feb 01, 2022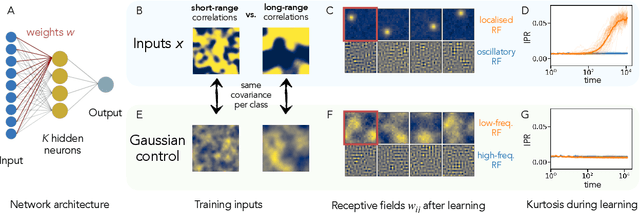
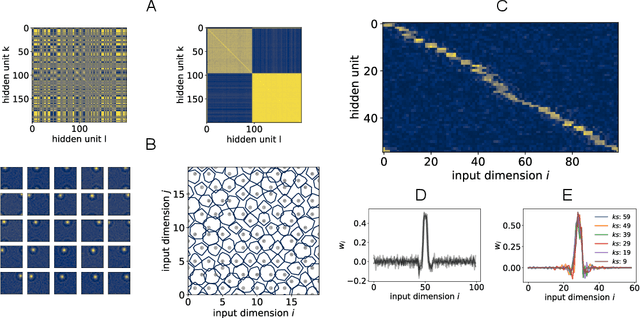
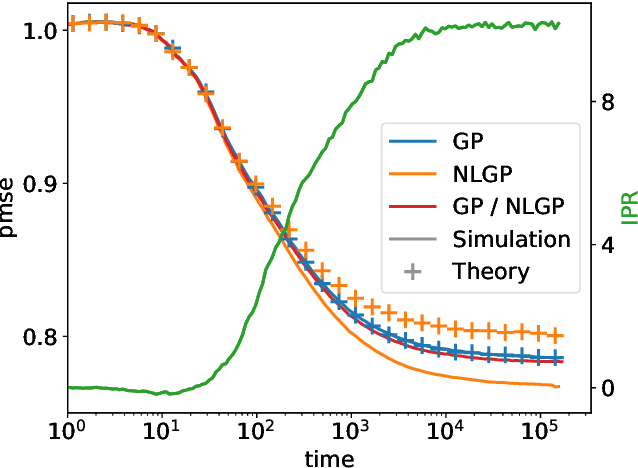
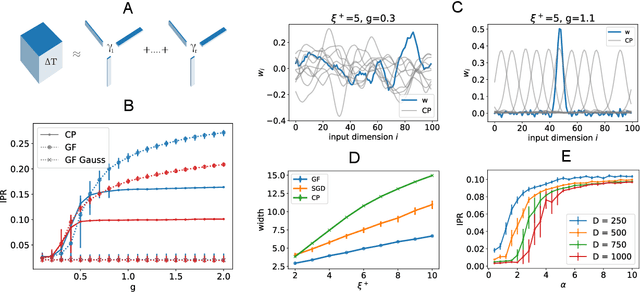
Exploiting data invariances is crucial for efficient learning in both artificial and biological neural circuits. Understanding how neural networks can discover appropriate representations capable of harnessing the underlying symmetries of their inputs is thus crucial in machine learning and neuroscience. Convolutional neural networks, for example, were designed to exploit translation symmetry and their capabilities triggered the first wave of deep learning successes. However, learning convolutions directly from translation-invariant data with a fully-connected network has so far proven elusive. Here, we show how initially fully-connected neural networks solving a discrimination task can learn a convolutional structure directly from their inputs, resulting in localised, space-tiling receptive fields. These receptive fields match the filters of a convolutional network trained on the same task. By carefully designing data models for the visual scene, we show that the emergence of this pattern is triggered by the non-Gaussian, higher-order local structure of the inputs, which has long been recognised as the hallmark of natural images. We provide an analytical and numerical characterisation of the pattern-formation mechanism responsible for this phenomenon in a simple model, which results in an unexpected link between receptive field formation and the tensor decomposition of higher-order input correlations. These results provide a new perspective on the development of low-level feature detectors in various sensory modalities, and pave the way for studying the impact of higher-order statistics on learning in neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge