Optimal Learning with Excitatory and Inhibitory synapses
Paper and Code
May 25, 2020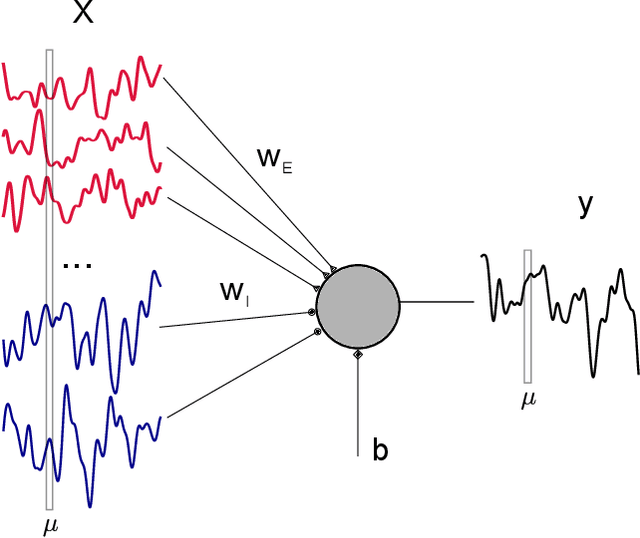
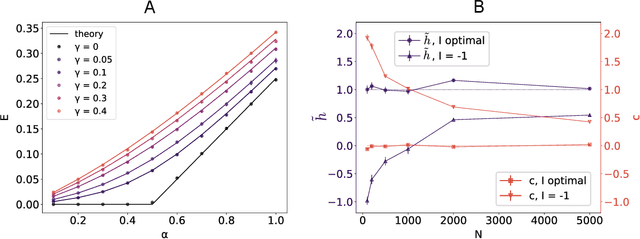
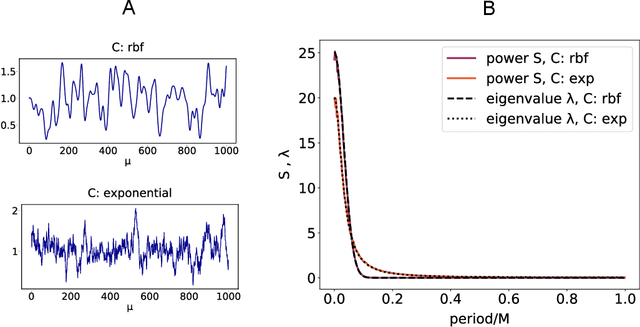
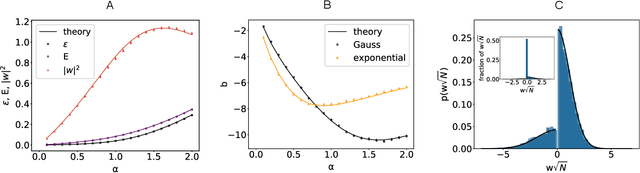
Characterizing the relation between weight structure and input/output statistics is fundamental for understanding the computational capabilities of neural circuits. In this work, I study the problem of storing associations between analog signals in the presence of correlations, using methods from statistical mechanics. I characterize the typical learning performance in terms of the power spectrum of random input and output processes. I show that optimal synaptic weight configurations reach a capacity of 0.5 for any fraction of excitatory to inhibitory weights and have a peculiar synaptic distribution with a finite fraction of silent synapses. I further provide a link between typical learning performance and principal components analysis in single cases. These results may shed light on the synaptic profile of brain circuits, such as cerebellar structures, that are thought to engage in processing time-dependent signals and performing on-line prediction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge