Matrix completion based on Gaussian belief propagation

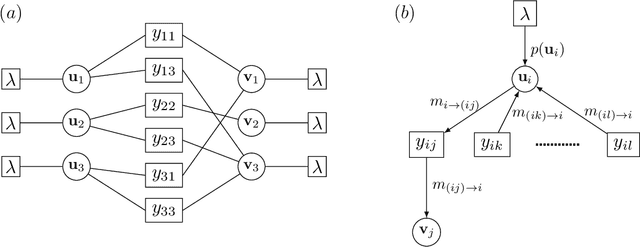
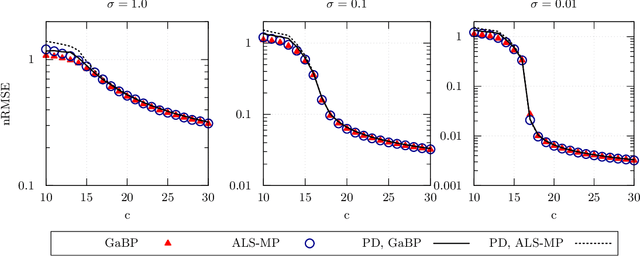
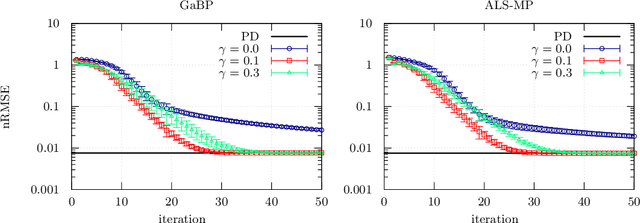
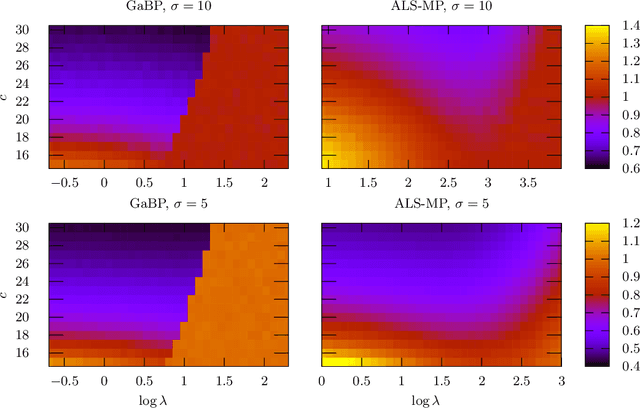
We develop a message-passing algorithm for noisy matrix completion problems based on matrix factorization. The algorithm is derived by approximating message distributions of belief propagation with Gaussian distributions that share the same first and second moments. We also derive a memory-friendly version of the proposed algorithm by applying a perturbation treatment commonly used in the literature of approximate message passing. In addition, a damping technique, which is demonstrated to be crucial for optimal performance, is introduced without computational strain, and the relationship to the message-passing version of alternating least squares, a method reported to be optimal in certain settings, is discussed. Experiments on synthetic datasets show that while the proposed algorithm quantitatively exhibits almost the same performance under settings where the earlier algorithm is optimal, it is advantageous when the observed datasets are corrupted by non-Gaussian noise. Experiments on real-world datasets also emphasize the performance differences between the two algorithms.