The Effect of Optimal Self-Distillation in Noisy Gaussian Mixture Model

Self-distillation (SD), a technique where a model refines itself from its own predictions, has garnered attention as a simple yet powerful approach in machine learning. Despite its widespread use, the mechanisms underlying its effectiveness remain unclear. In this study, we investigate the efficacy of hyperparameter-tuned multi-stage SD in binary classification tasks with noisy labeled Gaussian mixture data, utilizing a replica theory. Our findings reveals that the primary driver of SD's performance improvement is denoising through hard pseudo-labels, with the most notable gains observed in moderately sized datasets. We also demonstrate the efficacy of practical heuristics, such as early stopping for extracting meaningful signal and bias fixation for imbalanced data. These results provide both theoretical guarantees and practical insights, advancing our understanding and application of SD in noisy settings.

A replica analysis of under-bagging

A sharp asymptotics of the under-bagging (UB) method, which is a popular ensemble learning method for training classifiers from an imbalanced data, is derived and used to compare with several other standard methods for learning from imbalanced data, in the scenario where a linear classifier is trained from a binary mixture data. The methods compared include the under-sampling (US) method, which trains a model using a single realization of the subsampled dataset, and the simple weighting (SW) method, which trains a model with a weighted loss on the entire data. It is shown that the performance of UB is improved by increasing the size of the majority class, even if the class imbalance can be large, especially when the size of the minority class is small. This is in contrast to US, whose performance does not change as the size of the majority class increases, and SW, whose performance decreases as the imbalance increases. These results are different from the case of the naive bagging in training generalized linear models without considering the structure of class imbalance, indicating the intrinsic difference between the ensembling and the direct regularization on the parameters.

Asymptotic Dynamics of Alternating Minimization for Non-Convex Optimization

This study investigates the asymptotic dynamics of alternating minimization applied to optimize a bilinear non-convex function with normally distributed covariates. We employ the replica method from statistical physics in a multi-step approach to precisely trace the algorithm's evolution. Our findings indicate that the dynamics can be described effectively by a two--dimensional discrete stochastic process, where each step depends on all previous time steps, revealing a memory dependency in the procedure. The theoretical framework developed in this work is broadly applicable for the analysis of various iterative algorithms, extending beyond the scope of alternating minimization.

Compressed Sensing Radar Detectors based on Weighted LASSO

The compressed sensing (CS) model can represent the signal recovery process of a large number of radar systems. The detection problem of such radar systems has been studied in many pieces of literature through the technology of debiased least absolute shrinkage and selection operator (LASSO). While naive LASSO treats all the entries equally, there are many applications in which prior information varies depending on each entry. Weighted LASSO, in which the weights of the regularization terms are tuned depending on the entry-dependent prior, is proven to be more effective with the prior information by many researchers. In the present paper, existing results obtained by methods of statistical mechanics are utilized to derive the debiased weighted LASSO estimator for randomly constructed row-orthogonal measurement matrices. Based on this estimator, we construct a detector, termed the debiased weighted LASSO detector (DWLD), for CS radar systems and prove its advantages. The threshold of this detector can be calculated by false alarm rate, which yields better detection performance than the naive weighted LASSO detector (NWLD) under the Neyman-Pearson principle. The improvement of the detection performance brought by tuning weights is demonstrated by numerical experiments. With the same false alarm rate, the detection probability of DWLD is obviously higher than those of NWLD and the debiased (non-weighted) LASSO detector (DLD).

Average case analysis of Lasso under ultra-sparse conditions

We analyze the performance of the least absolute shrinkage and selection operator (Lasso) for the linear model when the number of regressors $N$ grows larger keeping the true support size $d$ finite, i.e., the ultra-sparse case. The result is based on a novel treatment of the non-rigorous replica method in statistical physics, which has been applied only to problem settings where $N$ ,$d$ and the number of observations $M$ tend to infinity at the same rate. Our analysis makes it possible to assess the average performance of Lasso with Gaussian sensing matrices without assumptions on the scaling of $N$ and $M$, the noise distribution, and the profile of the true signal. Under mild conditions on the noise distribution, the analysis also offers a lower bound on the sample complexity necessary for partial and perfect support recovery when $M$ diverges as $M = O(\log N)$. The obtained bound for perfect support recovery is a generalization of that given in previous literature, which only considers the case of Gaussian noise and diverging $d$. Extensive numerical experiments strongly support our analysis.

Compressed sensing radar detectors under the row-orthogonal design model: a statistical mechanics perspective

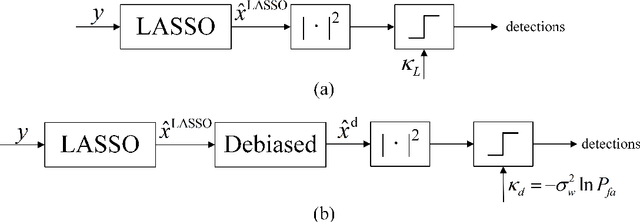
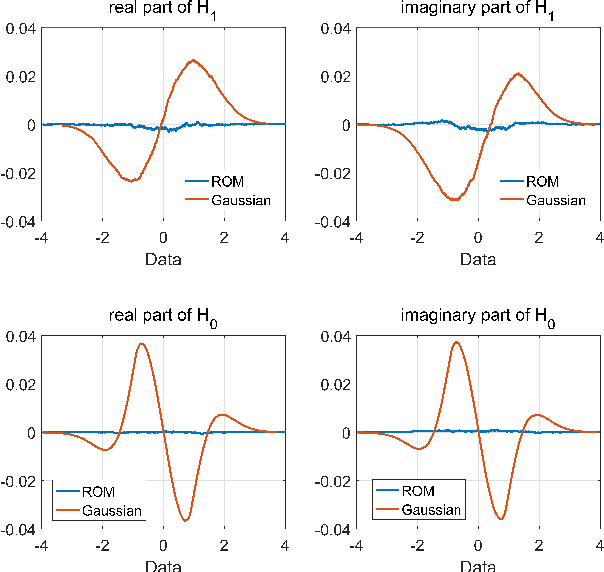
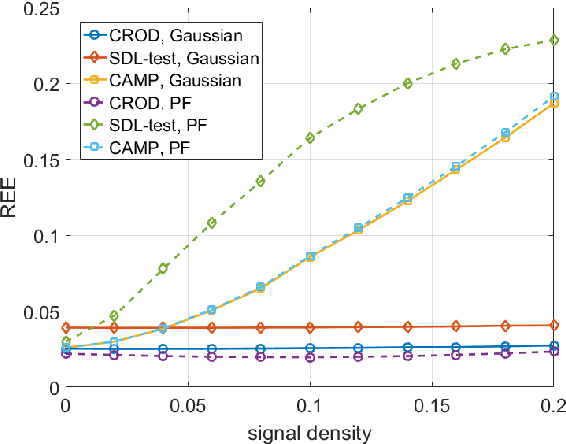
Compressed sensing (CS) model of complex-valued data can represent the signal recovery process of a large amount types of radar systems, especially when the measurement matrix is row-orthogonal. Based on debiased least absolute shrinkage and selection operator (LASSO), detection problem under Gaussian random design model, i.e. the elements of measurement matrix are drawn from Gaussian distribution, is studied by literature. However, we find that these approaches are not suitable for row-orthogonal measurement matrices, which are of more practical relevance. In view of statistical mechanics approaches, we provide derivations of more accurate test statistics and thresholds (or p-values) under the row-orthogonal design model, and theoretically analyze the detection performance of the present detector. Such detector can analytically provide the threshold according to given false alarm rate, which is not possible with the conventional CS detector, and the detection performance is proved to be better than that of the traditional LASSO detector. Comparing with other debiased LASSO based detectors, simulation results indicate that the proposed approach can achieve more accurate probability of false alarm when the measurement matrix is row-orthogonal, leading to better detection performance under Neyman-Pearson principle.

Sharp Asymptotics of Self-training with Linear Classifier

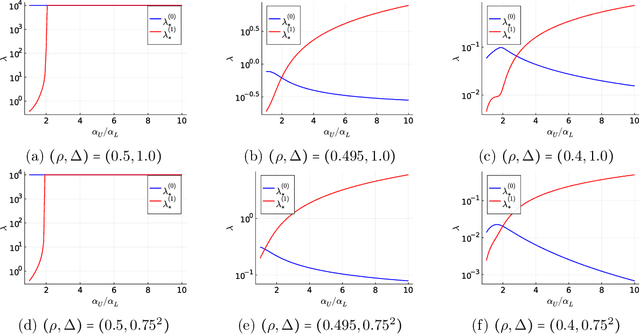
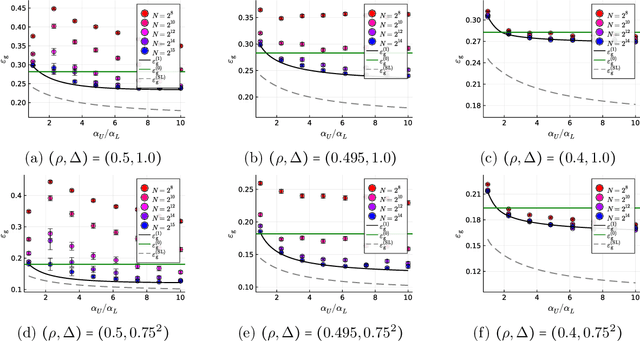
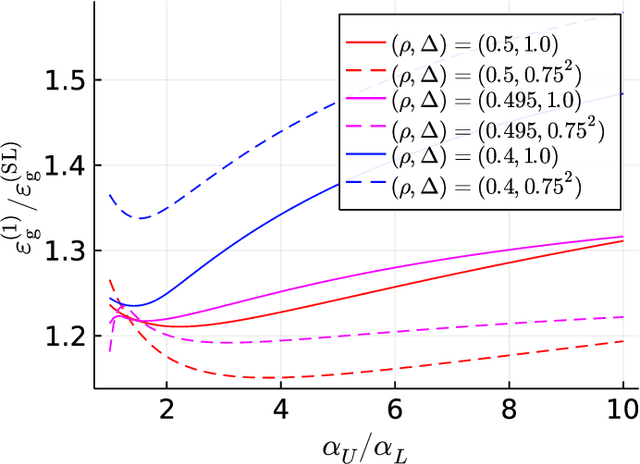
Self-training (ST) is a straightforward and standard approach in semi-supervised learning, successfully applied to many machine learning problems. The performance of ST strongly depends on the supervised learning method used in the refinement step and the nature of the given data; hence, a general performance guarantee from a concise theory may become loose in a concrete setup. However, the theoretical methods that sharply predict how the performance of ST depends on various details for each learning scenario are limited. This study develops a novel theoretical framework for sharply characterizing the generalization abilities of the models trained by ST using the non-rigorous replica method of statistical physics. We consider the ST of the linear model that minimizes the ridge-regularized cross-entropy loss when the data are generated from a two-component Gaussian mixture. Consequently, we show that the generalization performance of ST in each iteration is sharply characterized by a small finite number of variables, which satisfy a set of deterministic self-consistent equations. By numerically solving these self-consistent equations, we find that ST's generalization performance approaches to the supervised learning method with a very simple regularization schedule when the label bias is small and a moderately large number of iterations are used.

Semi-analytic approximate stability selection for correlated data in generalized linear models

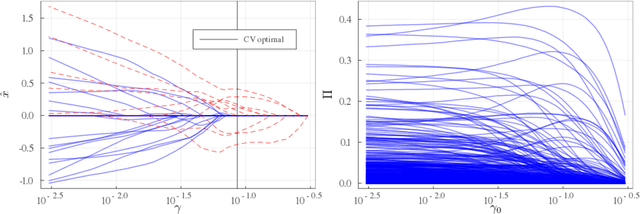
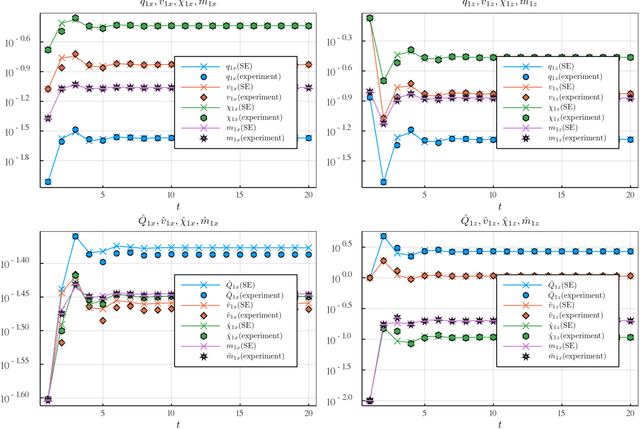
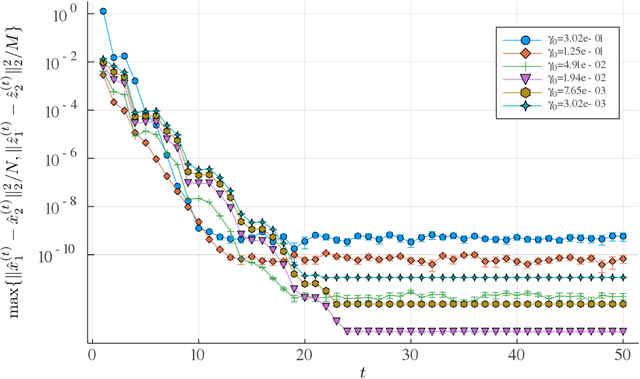
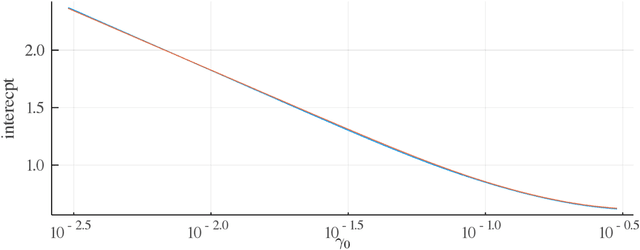
We consider the variable selection problem of generalized linear models (GLMs). Stability selection (SS) is a promising method proposed for solving this problem. Although SS provides practical variable selection criteria, it is computationally demanding because it needs to fit GLMs to many re-sampled datasets. We propose a novel approximate inference algorithm that can conduct SS without the repeated fitting. The algorithm is based on the replica method of statistical mechanics and vector approximate message passing of information theory. For datasets characterized by rotation-invariant matrix ensembles, we derive state evolution equations that macroscopically describe the dynamics of the proposed algorithm. We also show that their fixed points are consistent with the replica symmetric solution obtained by the replica method. Numerical experiments indicate that the algorithm exhibits fast convergence and high approximation accuracy for both synthetic and real-world data.

Replicated Vector Approximate Message Passing For Resampling Problem

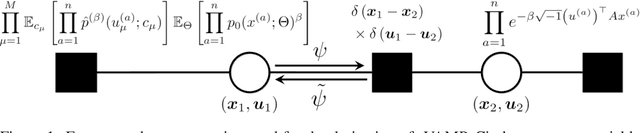
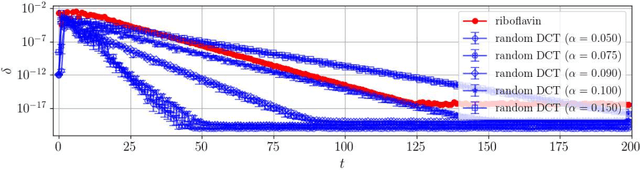
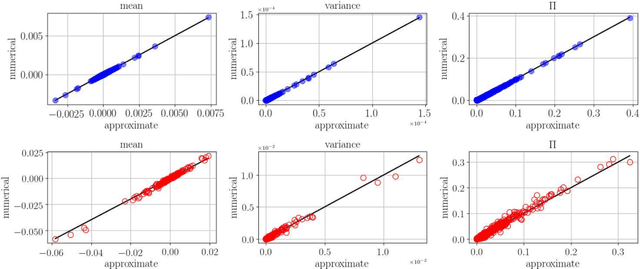
Resampling techniques are widely used in statistical inference and ensemble learning, in which estimators' statistical properties are essential. However, existing methods are computationally demanding, because repetitions of estimation/learning via numerical optimization/integral for each resampled data are required. In this study, we introduce a computationally efficient method to resolve such problem: replicated vector approximate message passing. This is based on a combination of the replica method of statistical physics and an accurate approximate inference algorithm, namely the vector approximate message passing of information theory. The method provides tractable densities without repeating estimation/learning, and the densities approximately offer an arbitrary degree of the estimators' moment in practical time. In the experiment, we apply the proposed method to the stability selection method, which is commonly used in variable selection problems. The numerical results show its fast convergence and high approximation accuracy for problems involving both synthetic and real-world datasets.