Sharp Asymptotics of Self-training with Linear Classifier
Paper and Code
May 16, 2022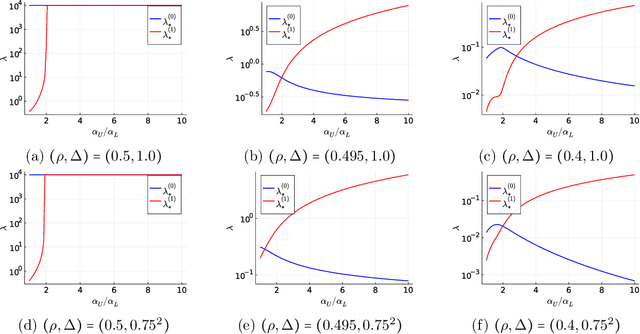

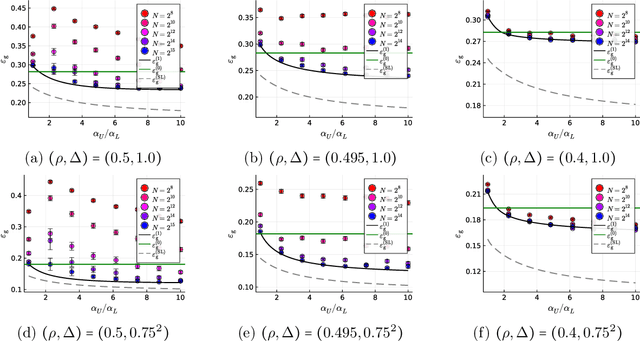
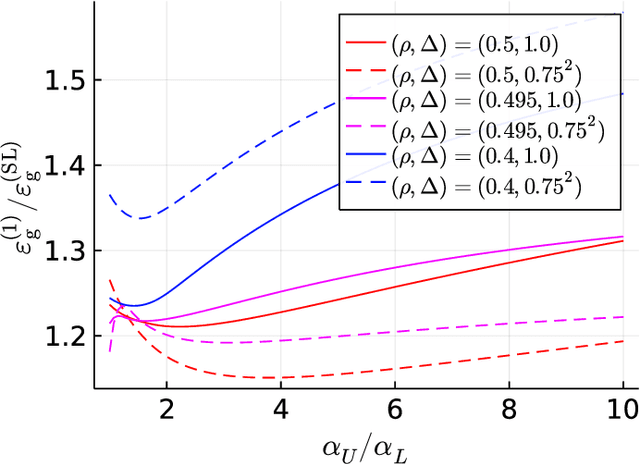
Self-training (ST) is a straightforward and standard approach in semi-supervised learning, successfully applied to many machine learning problems. The performance of ST strongly depends on the supervised learning method used in the refinement step and the nature of the given data; hence, a general performance guarantee from a concise theory may become loose in a concrete setup. However, the theoretical methods that sharply predict how the performance of ST depends on various details for each learning scenario are limited. This study develops a novel theoretical framework for sharply characterizing the generalization abilities of the models trained by ST using the non-rigorous replica method of statistical physics. We consider the ST of the linear model that minimizes the ridge-regularized cross-entropy loss when the data are generated from a two-component Gaussian mixture. Consequently, we show that the generalization performance of ST in each iteration is sharply characterized by a small finite number of variables, which satisfy a set of deterministic self-consistent equations. By numerically solving these self-consistent equations, we find that ST's generalization performance approaches to the supervised learning method with a very simple regularization schedule when the label bias is small and a moderately large number of iterations are used.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge