Plug-and-Play Latent Diffusion for Electromagnetic Inverse Scattering with Application to Brain Imaging

Electromagnetic (EM) imaging is an important tool for non-invasive sensing with low-cost and portable devices. One emerging application is EM stroke imaging, which enables early diagnosis and continuous monitoring of brain strokes. Quantitative imaging is achieved by solving an inverse scattering problem (ISP) that reconstructs permittivity and conductivity maps from measurements. In general, the reconstruction accuracy is limited by its inherent nonlinearity and ill-posedness. Existing methods, including learning-free and learning-based approaches, fail to either incorporate complicated prior distributions or provide theoretical guarantees, posing difficulties in balancing interpretability, distortion error, and reliability. To overcome these limitations, we propose a posterior sampling method based on latent diffusion for quantitative EM brain imaging, adapted from a generative plug-and-play (PnP) posterior sampling framework. Our approach allows to flexibly integrate prior knowledge into physics-based inversion without requiring paired measurement-label datasets. We first learn the prior distribution of targets from an unlabeled dataset, and then incorporate the learned prior into posterior sampling. In particular, we train a latent diffusion model on permittivity and conductivity maps to capture their prior distribution. Then, given measurements and the forward model describing EM wave physics, we perform posterior sampling by alternating between two samplers that respectively enforce the likelihood and prior distributions. Finally, reliable reconstruction is obtained through minimum mean squared error (MMSE) estimation based on the samples. Experimental results on brain imaging demonstrate that our approach achieves state-of-the-art performance in reconstruction accuracy and structural similarity while maintaining high measurement fidelity.

Fundamental Limit of Angular Resolution in Partly Calibrated Arrays with Position Errors

We consider high angular resolution detection using distributed mobile platforms implemented with so-called partly calibrated arrays, where position errors between subarrays exist and the counterparts within each subarray are ideally calibrated. Since position errors between antenna arrays affect the coherent processing of measurements from these arrays, it is commonly believed that its angular resolution is influenced. A key question is whether and how much the angular resolution of partly calibrated arrays is affected by the position errors, in comparison with ideally calibrated arrays. To address this fundamental problem, we theoretically illustrate that partly calibrated arrays approximately achieve high angular resolution. Our analysis uses a special characteristic of Cramer-Rao lower bound (CRB) w.r.t. the source separation: When the source separation increases, the CRB first declines rapidly, then plateaus out, and the turning point is close to the angular resolution limit. This means that the turning point of CRB can be used to indicate angular resolution. We then theoretically analyze the declining and plateau phases of CRB, and explain that the turning point of CRB in partly calibrated arrays is close to the angular resolution limit of distributed arrays without errors, demonstrating high resolution ability. This work thus provides a theoretical guarantee for the high-resolution performance of distributed antenna arrays in mobile platforms.

Approximating Multi-Dimensional and Multiband Signals

We study the problem of representing a discrete tensor that comes from finite uniform samplings of a multi-dimensional and multiband analog signal. Particularly, we consider two typical cases in which the shape of the subbands is cubic or parallelepipedic. For the cubic case, by examining the spectrum of its corresponding time- and band-limited operators, we obtain a low-dimensional optimal dictionary to represent the original tensor. We further prove that the optimal dictionary can be approximated by the famous \ac{dpss} with certain modulation, leading to an efficient constructing method. For the parallelepipedic case, we show that there also exists a low-dimensional dictionary to represent the original tensor. We present rigorous proof that the numbers of atoms in both dictionaries are approximately equal to the dot of the total number of samplings and the total volume of the subbands. Our derivations are mainly focused on the \ac{2d} scenarios but can be naturally extended to high dimensions.

Compressed Sensing Radar Detectors based on Weighted LASSO

The compressed sensing (CS) model can represent the signal recovery process of a large number of radar systems. The detection problem of such radar systems has been studied in many pieces of literature through the technology of debiased least absolute shrinkage and selection operator (LASSO). While naive LASSO treats all the entries equally, there are many applications in which prior information varies depending on each entry. Weighted LASSO, in which the weights of the regularization terms are tuned depending on the entry-dependent prior, is proven to be more effective with the prior information by many researchers. In the present paper, existing results obtained by methods of statistical mechanics are utilized to derive the debiased weighted LASSO estimator for randomly constructed row-orthogonal measurement matrices. Based on this estimator, we construct a detector, termed the debiased weighted LASSO detector (DWLD), for CS radar systems and prove its advantages. The threshold of this detector can be calculated by false alarm rate, which yields better detection performance than the naive weighted LASSO detector (NWLD) under the Neyman-Pearson principle. The improvement of the detection performance brought by tuning weights is demonstrated by numerical experiments. With the same false alarm rate, the detection probability of DWLD is obviously higher than those of NWLD and the debiased (non-weighted) LASSO detector (DLD).

Hybrid RIS-Assisted MIMO Dual-Function Radar-Communication System

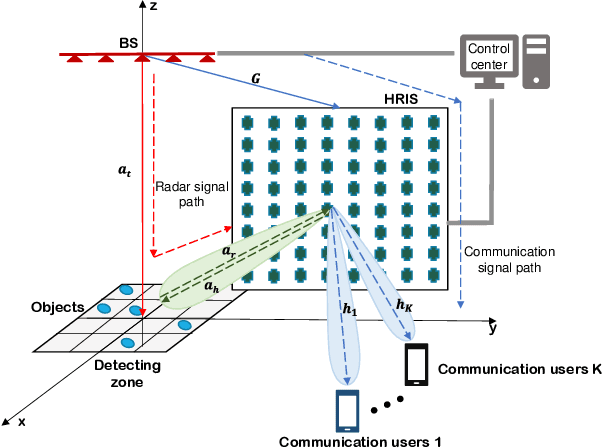
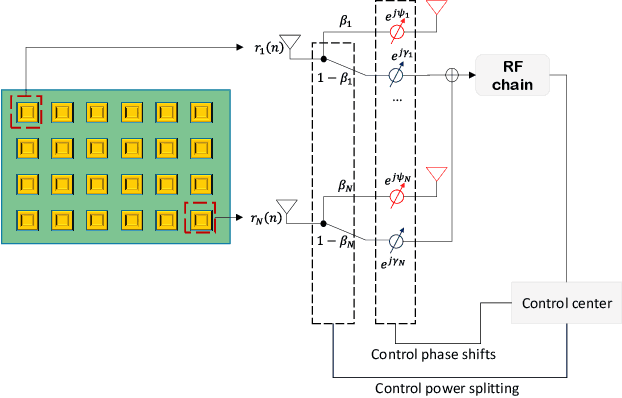
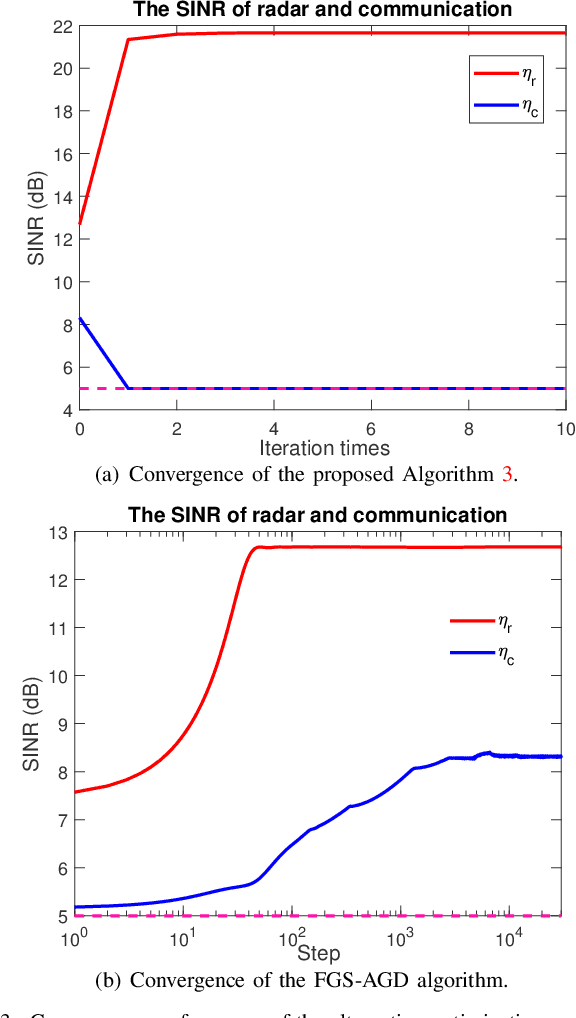
Dual-function radar-communication (DFRC) technology is emerging in next-generation wireless systems. Reconfigurable intelligent surface (RIS) arrays have been suggested as a crucial sensor component of the DFRC. In this paper, we propose a hybrid RIS (HRIS)-assisted multiple-input multiple-output (MIMO) DFRC system, where the HRIS is capable of reflecting communication signals to mobile users and receiving the scattering signal reflected from the radar target simultaneously. Under such a scenario, we are interested in characterizing the fundamental trade-off between radar sensing and communication. Specifically, we study the joint design of the beamforming vectors at the base station (BS) and the parameter configuration of the HRIS so as to maximize the signal-to-interference-and-noise ratio (SINR) of the radar while guaranteeing a communication SINR requirement. To solve the formulated non-convex beamforming design problem, we propose an efficient alternating optimization approach. In particular, for fixed beams at the BS, we use a fast grid search-assisted auto gradient descent (FGS-AGD) algorithm to seek the best HRIS configuration; Then, a closed-form BS beamforming solution is obtained using semidefinite relaxation. Numerical results indicate that compared with benchmark schemes, the proposed approach is capable of improving the radar performance and communication quality significantly and simultaneously.

a cognitive frequency allocation strategy for multi-carrier radar against communication interference

Modern radars often adopt multi-carrier waveform which has been widely discussed in the literature. However, with the development of civil communication, more and more spectrum resource has been occupied by communication networks. Thus, avoiding the interference from communication users is an important and challenging task for the application of multi-carrier radar. In this paper, a novel frequency allocation strategy based on the historical experiences is proposed, which is formulated as a Markov decision process (MDP). In a decision step, the multi-carrier radar needs to choose more than one frequencies, leading to a combinatorial action space. To address this challenge, we use a novel iteratively selecting technique which breaks a difficult decision task into several easy tasks. Moreover, an efficient deep reinforcement learning algorithm is adopted to handle the complicated spectrum dynamics. Numerical results show that our proposed method outperforms the existing ones.

Direction Finding in Partly Calibrated Arrays Exploiting the Whole Array Aperture

We consider the problem of direction finding using partly calibrated arrays, a distributed subarray with position errors between subarrays. The key challenge is to enhance angular resolution in the presence of position errors. To achieve this goal, existing algorithms, such as subspace separation and sparse recovery, have to rely on multiple snapshots, which increases the burden of data transmission and the processing delay. Therefore, we aim to enhance angular resolution using only a single snapshot. To this end, we exploit the orthogonality of the signals of partly calibrated arrays. Particularly, we transform the signal model into a special multiple-measurement model, show that there is approximate orthogonality between the source signals in this model, and then use blind source separation to exploit the orthogonality. Simulation and experiment results both verify that our proposed algorithm achieves high angular resolution as distributed arrays without position errors, inversely proportional to the whole array aperture.

Towards a performance bound on MIMO DFRC systems

It is a fundamental problem to analyse the performance bound of multiple-input multiple-output (MIMO) dual-functional radar-communication (DFRC) systems. To this end, we derive a performance bound on the communication function under a constraint on radar performance. To facilitate the analysis, we consider a toy example, in which there is only one down-link user with a single receive antenna and one radar target. In such a simplified case, we obtain an analytical expression for the performance bound and the corresponding waveform design strategy to achieve the bound. The results reveal a tradeoff between communication and radar performance, and a condition when the transmitted energy can be shared between these two functions.

Compressed sensing radar detectors under the row-orthogonal design model: a statistical mechanics perspective

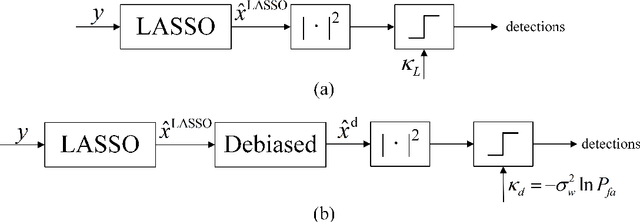
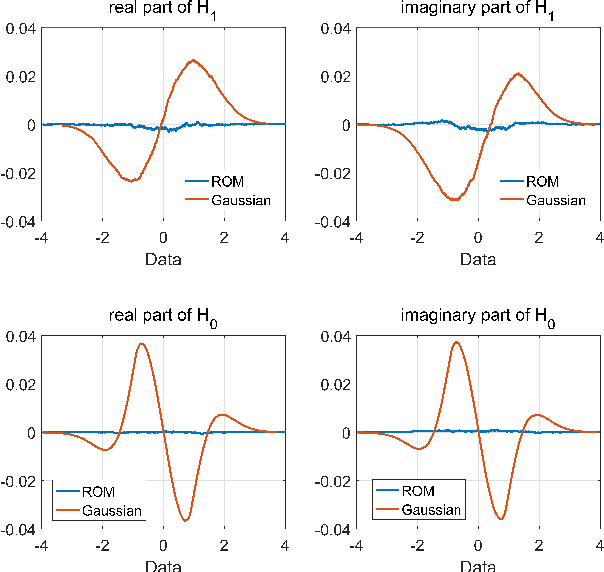
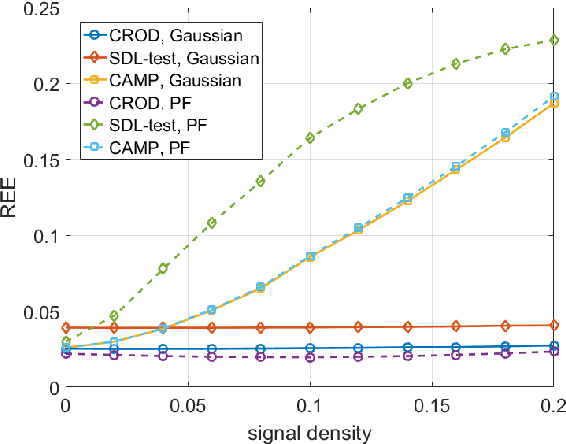
Compressed sensing (CS) model of complex-valued data can represent the signal recovery process of a large amount types of radar systems, especially when the measurement matrix is row-orthogonal. Based on debiased least absolute shrinkage and selection operator (LASSO), detection problem under Gaussian random design model, i.e. the elements of measurement matrix are drawn from Gaussian distribution, is studied by literature. However, we find that these approaches are not suitable for row-orthogonal measurement matrices, which are of more practical relevance. In view of statistical mechanics approaches, we provide derivations of more accurate test statistics and thresholds (or p-values) under the row-orthogonal design model, and theoretically analyze the detection performance of the present detector. Such detector can analytically provide the threshold according to given false alarm rate, which is not possible with the conventional CS detector, and the detection performance is proved to be better than that of the traditional LASSO detector. Comparing with other debiased LASSO based detectors, simulation results indicate that the proposed approach can achieve more accurate probability of false alarm when the measurement matrix is row-orthogonal, leading to better detection performance under Neyman-Pearson principle.

Physics Embedded Machine Learning for Electromagnetic Data Imaging

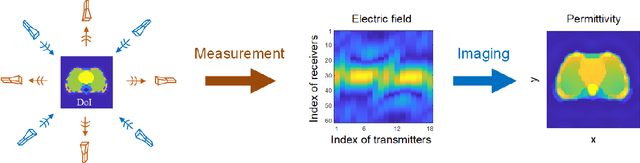
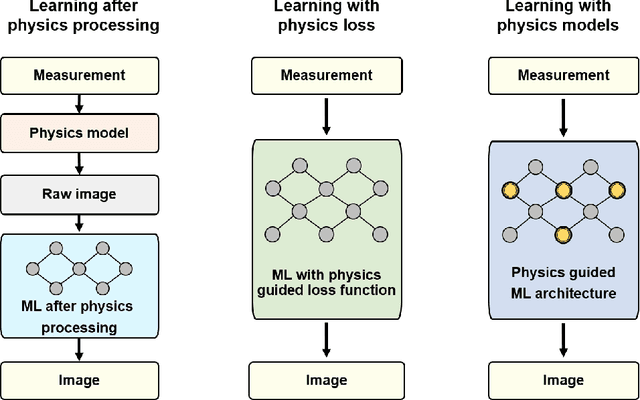
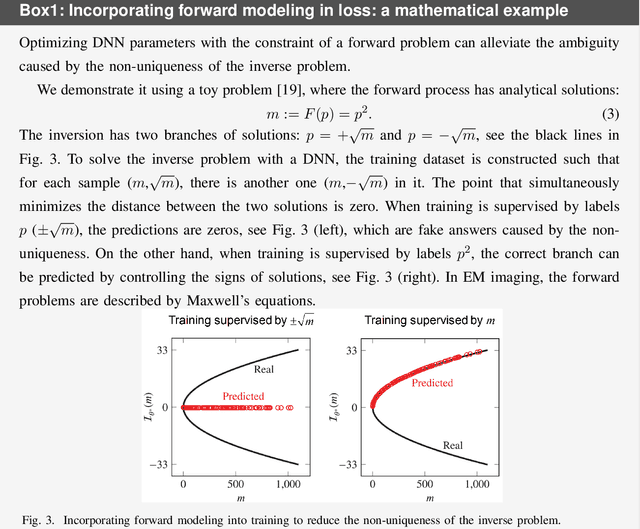
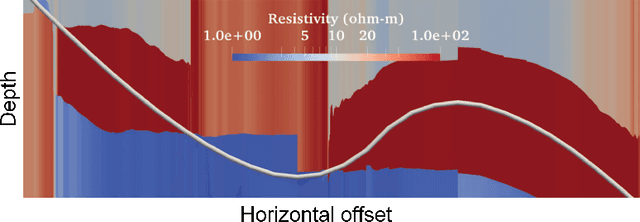
Electromagnetic (EM) imaging is widely applied in sensing for security, biomedicine, geophysics, and various industries. It is an ill-posed inverse problem whose solution is usually computationally expensive. Machine learning (ML) techniques and especially deep learning (DL) show potential in fast and accurate imaging. However, the high performance of purely data-driven approaches relies on constructing a training set that is statistically consistent with practical scenarios, which is often not possible in EM imaging tasks. Consequently, generalizability becomes a major concern. On the other hand, physical principles underlie EM phenomena and provide baselines for current imaging techniques. To benefit from prior knowledge in big data and the theoretical constraint of physical laws, physics embedded ML methods for EM imaging have become the focus of a large body of recent work. This article surveys various schemes to incorporate physics in learning-based EM imaging. We first introduce background on EM imaging and basic formulations of the inverse problem. We then focus on three types of strategies combining physics and ML for linear and nonlinear imaging and discuss their advantages and limitations. Finally, we conclude with open challenges and possible ways forward in this fast-developing field. Our aim is to facilitate the study of intelligent EM imaging methods that will be efficient, interpretable and controllable.